はじめに
今回は、Pythonのrandomモジュールについて解説します。
↓の内容を一般人が読めて分かるぐらいに、まとめなおしたモノになります。

Pythonの導入が済んでいて、基本操作が行えることを前提で進めます。
↓前提知識はこちらをご覧ください↓

ランダム処理の種類について
パソコンのランダムは…
ほとんどの場合で本当の意味で “ランダム” ではありません。
Pythonのランダム処理も同じです。
「疑似乱数生成法」という、特定の条件が揃えば結果を再現できる技術を使って作られてます。
【疑似乱数生成法】
・"ランダム" に見える数字を人工的に作り出す処理
・○○法のような様々な生成方法がある(詳細)
・パソコンのランダム処理の主流凄く雑に言うと「11,64,19,33,78」みたいな適当な “固定された” 数字を使ってます

パソコンは「0」と「1」の組み合わを使った “計算” で作られてます。
なので、ランダムという “適当に” という処理な処理を行うのは難しいです。
この問題を解決するため “適当に” を計算で出せるようにしたモノが疑似乱数になります。
ちなみにPythonのrandomモジュールは「メルセンヌ・ツイスタ(MT法)」という疑似乱数生成法を使ってます。
MT法の詳細はこのあたりで解説されてましたが…
一般人が見ても、正直わからないモノでした。
そして、後で紹介する疑似乱数の内部の値(SEED値)に現在の時刻などを使う事で…
ほぼ同じ結果にならない「= “ランダム”」が作られている形になります。

これが、ランダム処理の種類です。
ランダムな整数を出す
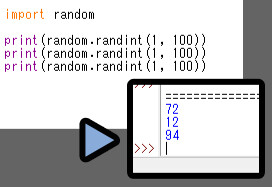
まず「import random」でpython内蔵のランダムモジュールを読み込みます。
そして「random.randint(0,100)」を使うと0~100の整数をランダムに出します。
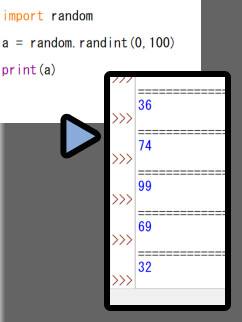
特別な設定をしてなければ、全ての数字が同じ確率で出ます。
↓このような出現方法を「一様分布」と呼びます。

そして、ランダムな整数は「random.randrange()」でも生成できます。
これは()に入れる数は1つだけです。
自動で0スタートになり、指定したい最大値を「(n+1)」の形で入力します。
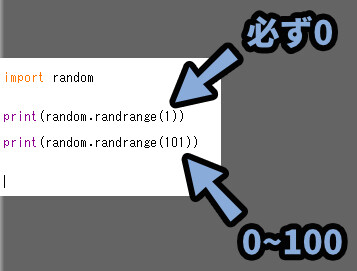

0~100を指定する場合は、n+1なので…
(0~101)と書く形になります。
これは、randrange()が0を “1” としてカウントしてる事の影響です。
そして.randint()と.randrange()は書き方が違うだけで…
内部的には同じ処理になります。

あと、randrange()に2つの値を渡すと、範囲で指定が可能です。

randrange()の範囲指定は、最初の値は「+1」”しない” こと。
そして、2番目の値にだけ「+1」”する” 事に注意。

(0,101)のように指定した場合…
→ 0~100になります。
(50,101)のように指定した場合…
→ 50~100になります。
なので、書き方としてはこちらが正解です。
「randrange(最小値 , 最大値+1)」
そして、randrange()は3つ目の要素「ステップ」を設定できます。
これを入れると「ステップの数×n」の値しか出力しなくなります。
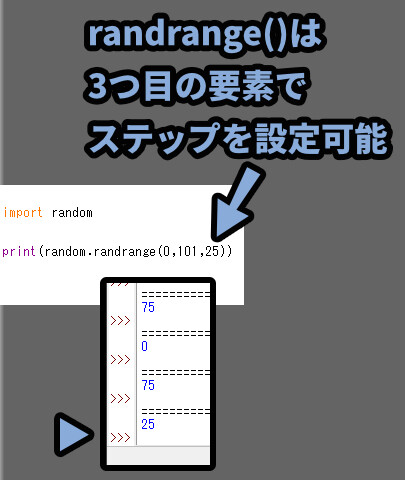
.randint()の方が直感的に分かりやすいと思います。
なので、基本は「.randint()」で大丈夫です。

ステップ処理が必要な時だけ…
.randrange()を使う事をおすすめします。
(果たして… ステップを使う場面は来るのだろうか…)
以上が、ランダムな整数を出す方法です。
リストから取り出す
randomモジュールは、リスト系の情報から要素を取り出す事ができます。
代表的なモノは「random.choice()です。」
これは、リストの中からランダムで1つの要素を取り出す処理になります。
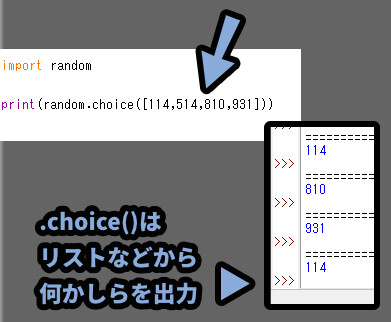
このような、リストを操作する処理は他にも3つあります。
・.sample() / 複数のモノを取り出す(重複なし)
・.choices() / 複数のモノを取り出す(重複あり)
・.shuffle() / リストの中身を混ぜるこちらを、解説していきます。
.sampleについて
.sample()もリストからランダムに取り出す処理です。
取り出すモノが1つの場合.choice()と同じ結果になります。

.choice()との違いは、取り出す要素の数を指定できる事です。
リストの後で「,n」のような数字を打ち込むと取り出す数を変えれます。
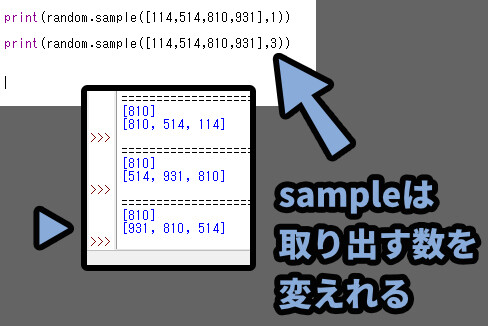
sample()は基本、同じものが2回取り出されないようになってます。
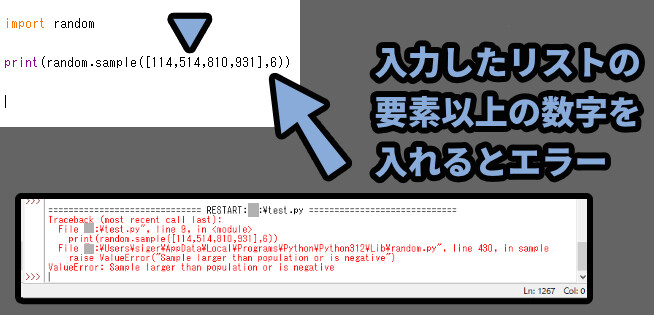
なので、入力したリストの要素以上の数字を入れるとエラーが出ます。
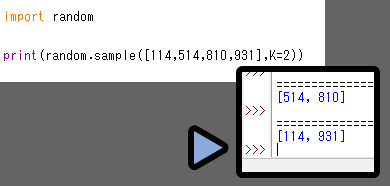
また、取りだす要素の数は「k=」という形でも指定可能です。
やってる事は、ほぼ同じになります。
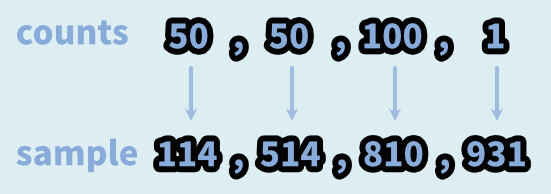
counts=[]を使えばリスト内から取り出せる確率を操作できます。
このcounts=[]を使う場合、取り出す数の指定は必ず「k=」という形で書く事ができます。


counts=[]を使った場合、重複が有効になるようになるので…
「k=」はリスト以上の数に設定できます。
(処理的には、たぶんリスト内の要素を設定したcountsの数だけ増やしてる…?
のかなぁと思います。)
「リストの要素の数」と「counts=[]の数」は必ず一致させてください。
でないと、エラーができます。
下図のように、リストの要素に確率の重みづけを行う処理になります。

この重みづけを使うよりも、random(1~100)を出して
if文で(1~30)なら実行みたいな形で処理した方が…
確率を「%」単位で操作できるので使いやすいと思います。
なので、countsはほぼ使わない。
→ sampleは重複無しの取り出しという認識で大丈夫と思います。
以上が、.sampleについての解説です。
.choicesについて
.sample()もリストからランダムに取り出す処理です。
リストを入れて、右側に「k=」という形で取り出す数を指定します。
こちらは “重複あり” の取り出し方になります。
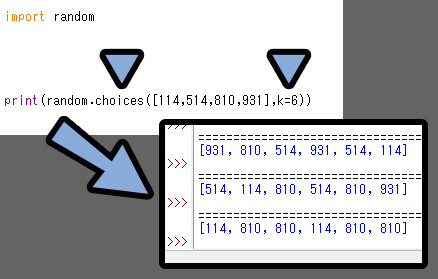
なので「k=」で指定した回数だけ抽選が行われて…
毎回、全てのリスト内から1つを選ぶという形で処理が行われてます。

取り出したものをリスト内に戻して、再度取り出してるイメージ。
あと、choices()は「k=」という形で回数を書かないとエラーが出ます。
「choices」だけ違う取り出し方になってます。
後で紹介する、乱数の内部状態を合わせる「Get/Set State」を使っても違う結果になります。
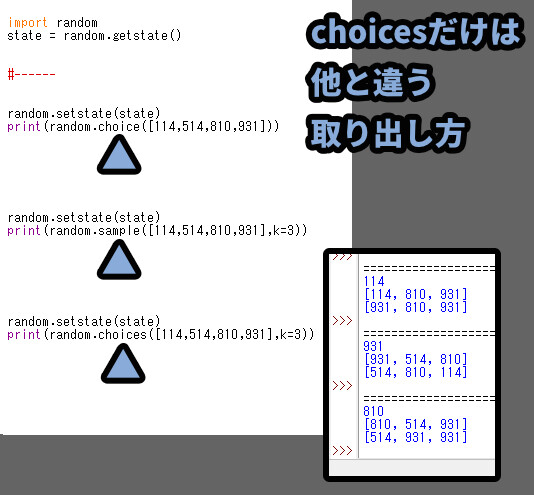

choices()とsample()は最初の1つだけ一致します。
「choices」も抽選確率を変えれます。
こちらは「weights=[]」を使って指定する形になります。
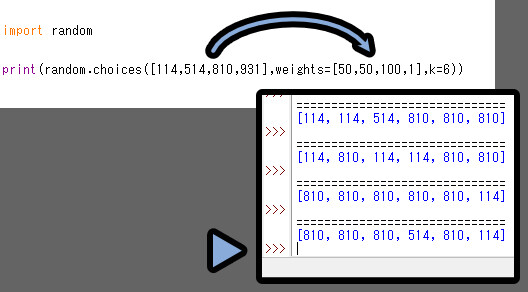
samlpe()の処理と考え方は同じです。
「リストの要素の数」と「weights=[]の数」は必ず一致させてください。
でないと、エラーができます。
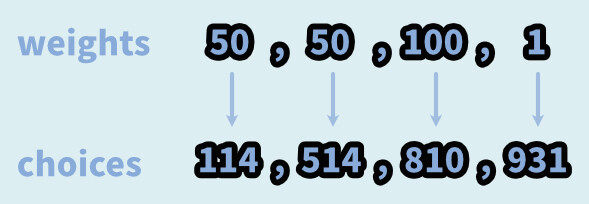
そしてweights=[]は、cum_weights=[]という方法でも表記できます。
これは同じ処理です。必要となる書き方が違うだけです。
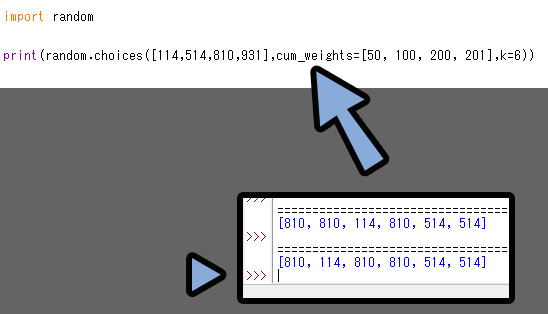
cum_weights=[]の場合、左との数字の差が確率になります。
ベースの数字に、数値を足して入力していくイメージです。
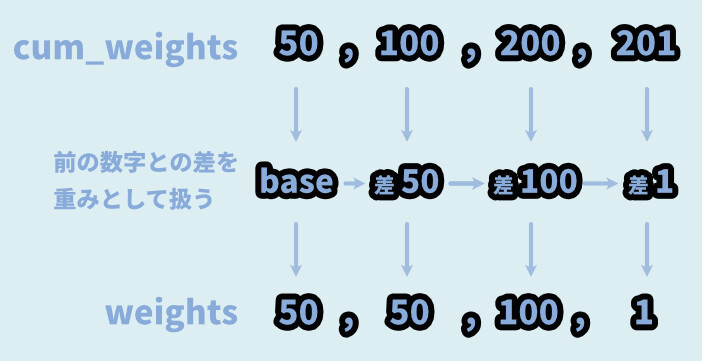
なので、下記の2つは同じ処理になります。
・weights=[50,50,100,1]
・cum_weights=[50,100,200,201]
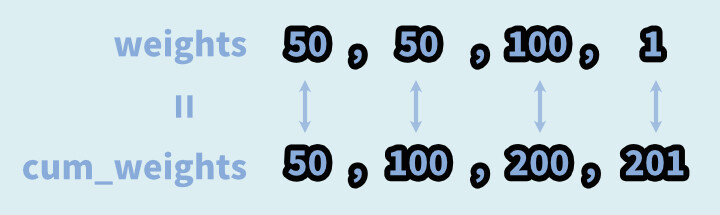
weights=[]の方が、直感的に書けます。(簡単)
ただ、パソコンは内部でcum_weights=[]の形に変換して処理してるようなので…
cum_weights[]の方が若干、高速です。

基本、weights=[]で良いと思います。
というより、randomで(1~100)を出して
if文で切り分けていく方が、扱いやすい。
なので、そもそも「weights」を使う機会が少ない気がします。
以上が、.choicesについての解説です。
.shuffleについて
.shuffleはリスト内のモノを混ぜる機能です。
これを行うと、リスト内に入れた情報の “順番が” ランダムに変わります。
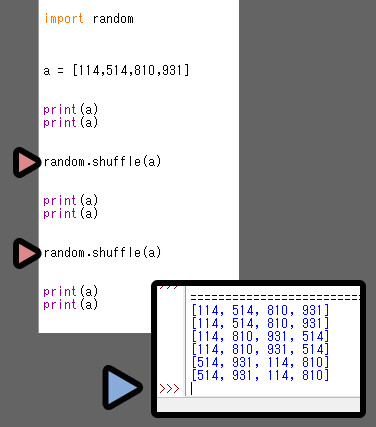
役割としては、これだけです。
以上が.shuffleについての解説です。
SEED値について
pythonのランダムは、厳密に言えば完璧な意味でのランダムではありません。
疑似乱数という複雑な数値の状態を “システム時刻” で決めて動かしてます。


OSが乱数用の値を提供してる場合は…
システム時刻ではなく、そちらが採用されるようです。
「SEED値」を操作すると、疑似乱数の内部状態は手動で決めることができます。
これはrandom.seed()で設定できます。
seedを設定すると、疑似乱数の内部状態が固定されるので同じ結果になります。
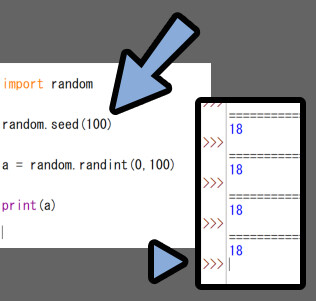
seed値は文字なども設定できます。
(たぶん、適当な数字に変換されて処理されてます)
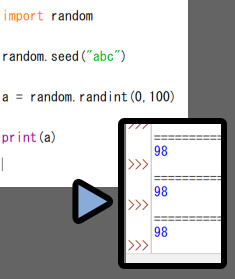
特に設定が無ければシステム時刻です。

「random.seed()」と「指定なし」の場合…
Pythonはシステム時刻で、疑似乱数の内部状態が決まります。

あとrandom.seed()は2つ目の要素でSEEDのバージョンを設定できます。
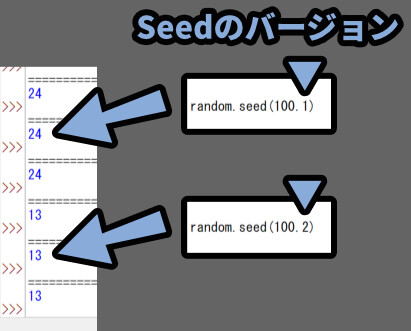
【バージョン1のシード】
・文字型とビット型を入れた時に整数に変換される
・この、整数変換時に生成される値の範囲がやや狭い
・古いPythonのランダムを再現するために用意されている
//ーーーーー
【バージョン2のシード】
・文字型とビット型を入れた時に整数に変換される
・この、整数変換時に生成される値の範囲が広い
・こっちの方が、新しくて性能が良いのでコレで良い
2の方が性能は良いっぽいですが…
わざわざ、シードのバージョンまで指定する機会は少ないよねという…。
以上が、SEED値についての解説です。
get/set stateについて
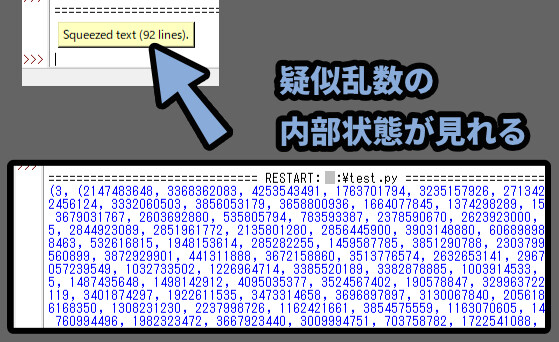
random.getstate()を使うと、疑似乱数の内部状態を “記録” できます。
print(random.getstate())を行うと、記録した疑似乱数の状態を出力できます。
IDLEへの出力は、文字が多すぎて折りたたまれてます。
「Squeezed test (92line).」をクリック。
すると、展開されて内部を確認できます。
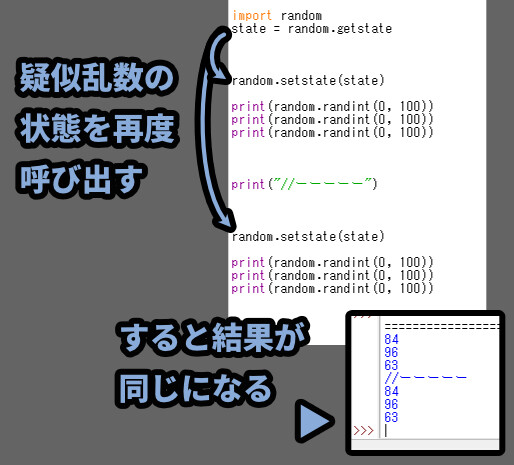
random.setstate()は記録した疑似乱数の状態を読み込んで “使える” ようにします。
任意の「変数」に = random.getstate()の情報を入れます。
そしてrandom.getstate(「変数」)のような形で使うのが一般的。

普段はこの乱数の記録 → 読み込みまで自動で行われてます。

なので、普通のランダム利用の場合、書かなくて大丈夫です。
ではなぜ「乱数の記録 → 読み込み」をわざわざ分けて書くかというと…
途中でもう一度、乱数の状態を最初から読み込むめ治せるからです。
これで “同じ処理” を繰り返すと… 同じ値が変えるようになります。
PCのランダムは、完全なランダムではないので疑似乱数という複雑な値が使われてます。
そして、先ほど見た乱数の内部状態から1番目はコレ、2番目はコレという形で決めてます。

乱数を再度呼び出すと、この “1番目” のカウントがリセットされます。
そして、また1番目からスタートするので、結果が同じになります。

ちなみに、先ほど触ったSEEDは内部状態を変える処理でした。
なので、途中でSEED変更をしてから、getstate()で乱数の状態を保存すると…
別の乱数を保存できます。
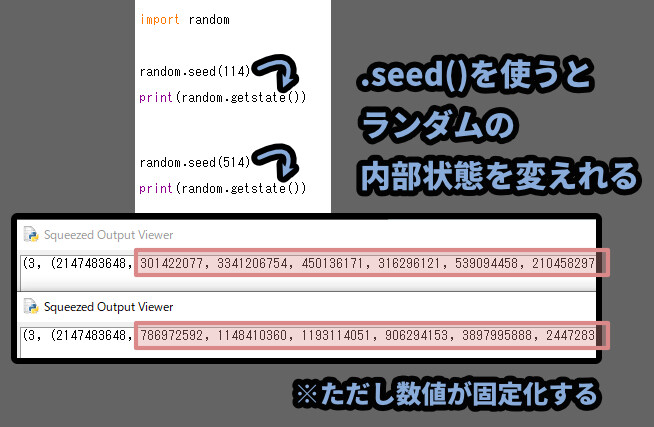

ただし、SEED値を固定するので…
システム時刻による “ランダム性” が失われます。
→ 時間をずらして実行しても、同じ結果になるので注意。
ちなみに、2つ以上ある内部情報は右クリックしないと表示されませんでした。
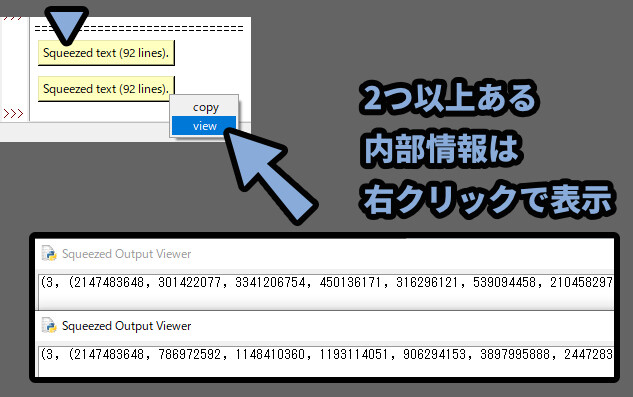
実験で下記の3通りを用意。
・① → SEED固定なし(システム時刻)
・②~➂ → SEED固定ありすると、①以外は何度実行しても、同じ結果になります。

以上が、get/set stateの使い方です。

これだけだと謎機能で終るので…
次はこの「get / set state」の使い方を解説します。
似た処理が “完全に同じ” なのかを調べる
「get / set state」を使うと、似てる処理が完全に同じなのかを確認できます。
例えば「choice」と「1つだけ取り出すsample」の上に…
乱数の状態をリセットする処理を入れます。
そして実行すると、同じ結果になります。


つまり、「choice」と「sample」の中で使われてる
ランダムの取り出し処理は同じモノのようです。
同様の条件で「choices」を追加。
さらに変化を見るために「sample」の値を3つに増やしました。
すると… 「choices」は乱数の条件を揃えても別の結果になります。


つまり「choices」はchoiceやsampleとは別の仕組みで
抽選結果を選んでると考えられます。
このように「get / set state」を使うと、似てる処理が完全に同じなのかを確認できます。
以上が「get / set state」の解説です。
その他のランダム出力(小数/Bit/文字)
random.は整数以外の情報も出力できます。
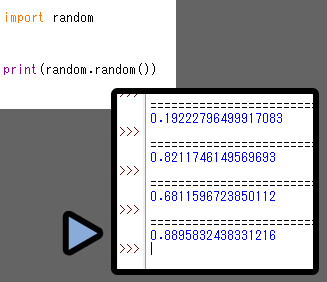
「random.random()」は小数0~1の値を返します。
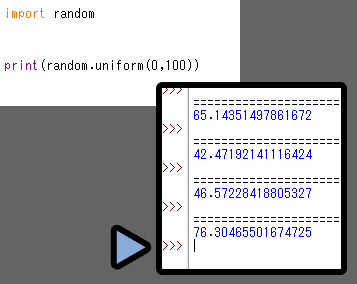
random.uniform(最小値, 最大値)も同様に小数を返します。
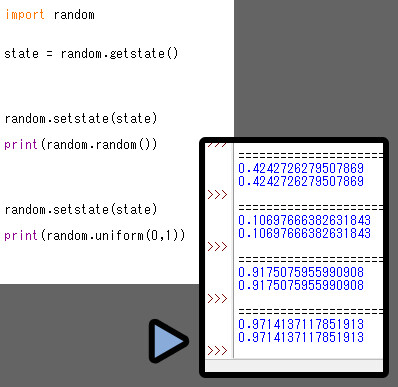
.random()と.uniform(0,1)の場合…
get/set stateで乱数を揃えると同じ結果になります。
→ 内部処理的には同じモノと分かります。

.uniform(最小値, 最大値)の方が数値指定ができるので優秀。
.random()には何も入れれないようです。
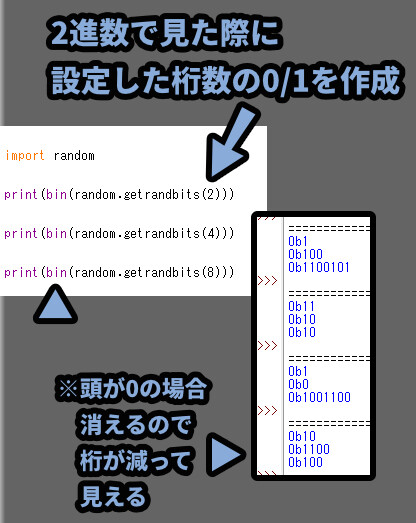
getrandbits(ビット数)は指定した数のビットだけ「0/1」の情報を作り出します。
頭が「0」だと消されるので… 8を指定しても省略されて0b100になる事があります。
ビットについての概念が分からない方、
より詳しく知りたい方はこちらをご覧ください。

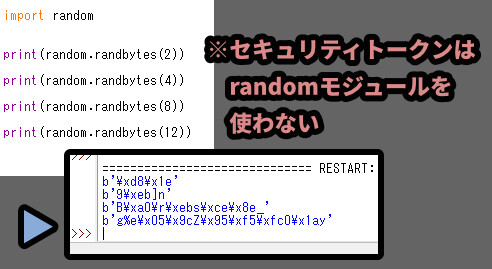
.randbytes(文字数)は指定した文字数の数だけ、ランダムな文字列を作り出します。
ただし、こちらはセキュリティ関係には使わないでください。
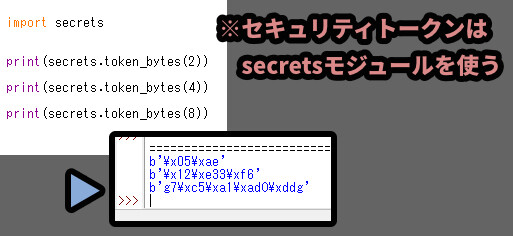
セキュリティ関係で文字列を使う場合…
Python側は「secrets」というモジュールを使う事をおすすめしてます。
import secrets
secrets.token_bytes(文字数) で作れます。

詳しい事は分からないですが、こちらの方が強固のようです。
(システム時刻、取られたらセキュリティが崩されるリスク回避かな…?)
以上が、その他の出力についての解説です。
結果の分布を変える
ランダムの結果に、特定のパターンを作ることができます。
このようなパターンを分布と言います。
例えば普通のランダムの場合…

一様分布という、すべて同じパターンになります。

このような、分布を見ていきます。

ちなみに、この分布は “統計学” を触る上で重要になります。
あと、これ以降のグラフは手描きで作ってるので…
厳密な”結果”とカーブの形が微妙に違う事があります。

あくまで、イメージを掴むモノとしてご覧ください。
(詳細は、統計学の専門書を見た方が良いです)
正規分布系
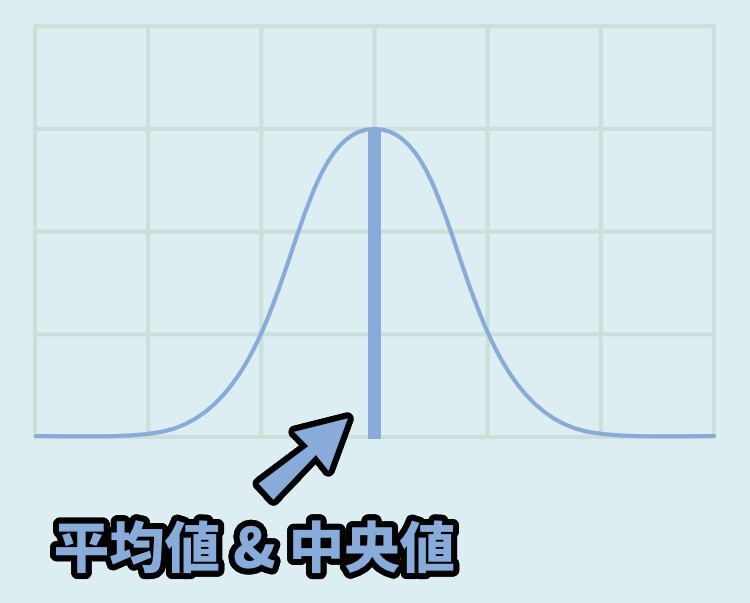
正規分布という形があります。
ベルカーブとも呼ばれる、平均的な人が多い形です。
人間の知能の分布などは、このベルカーブになると言われてます。
これは、平均と中央値がほぼ同じになると言われてます。
・平均値 → すべての数値を足してから、足した"数"を割る
(100人いたら、全部の値を足して÷100した値)
・中央値 → 全ての人の値を並べて、足した数÷2の人の値を取る
(100人いたら値が50番人目の人が持つ値)The普通の形です。
この正規分布っぽい形を作り出す、ランダム機能を紹介していきます。
二項分布
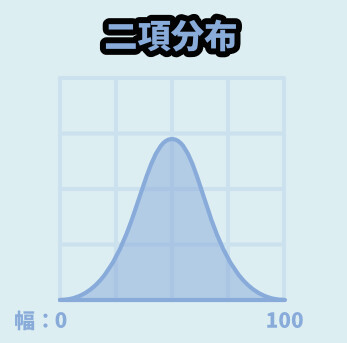
成功確率が50%の事を、100回やると考えます。
すると、成功数は下図のような分布になると言われてます。
これが「二項分布」になります。
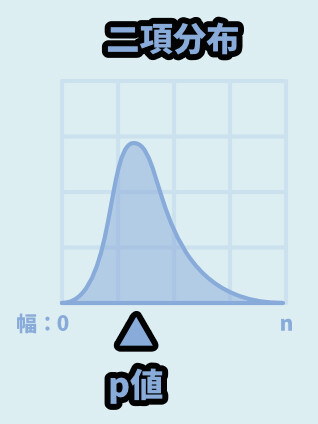
こちらは「random.binomialvariate(試行回数, 成功率)」という形で使えます。
・試行回数(n) = グラフの最大値と考えらえます
・成功率は0が0%~1が100%という形で表します(p値)

p値を動かすと、最大値の山が動きます。
以上が、二項分布についての解説です。
ガウス分布
一般的な正規分布の形になる方法です。
Pythonで正規分布を扱うなら、これがおすすめ。
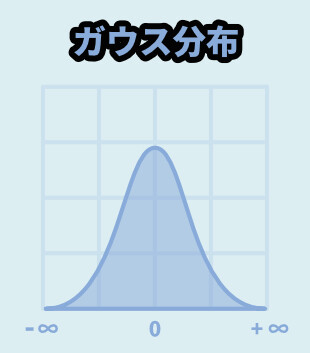
「random.gauss(数値の位置ズレ, 拡散率)」で表せます。
数値のズレが「0」であれば、0を中心に広がった形の分布になります。
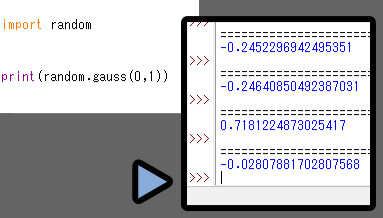

最大値と最小値の指定は無いようです。
なので、めったに起こらないですが…
たまにものすごく大きな、数値が出る可能性が残されてます。
数値のズレ(μ / ミュー)を操作すると、分布の開始位置がズレます。
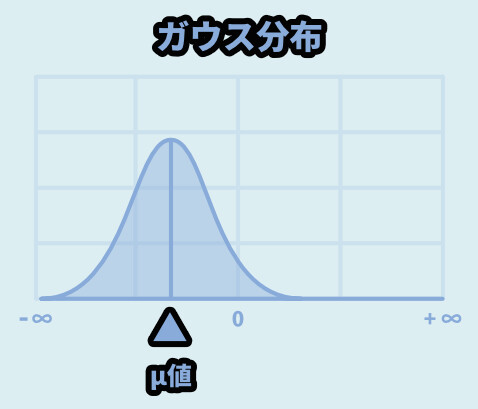
μ = 100にすると、100を軸に分布が始まります。
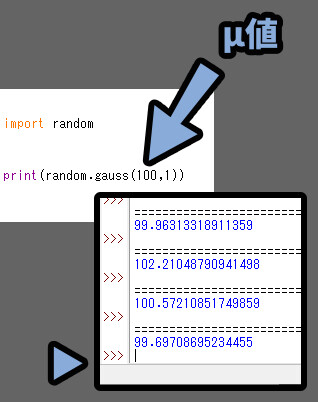
拡散率(σ / シグマ)を操作すると、山の形が変わります。
σ値が大きいほど、分散が広がり数値の差が出やすくなります。
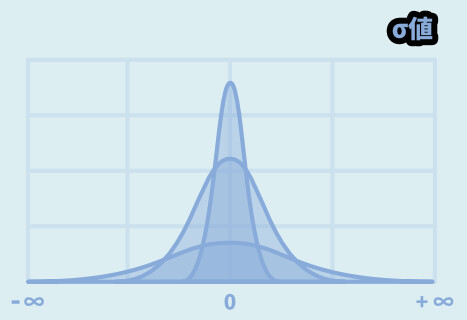
試しに、σ値を「100」に設定。
すると、+62や-52のような大きな数字が出ることが分かります。

以上が、ガウス分布です。
正規分布
正規分布を作るための処理です。
表現する数式や内部処理が違いますが、動きはガウス分布とほぼ同じとされてます。

パラメーターや考え方も、ガウス分布とほぼ同じです。
random.normalvariate(μ, σ)
・μ → 数値のズレ
・σ → 拡散率ただ、内部処理が違うので乱数の状態を揃えても結果は別物になります。
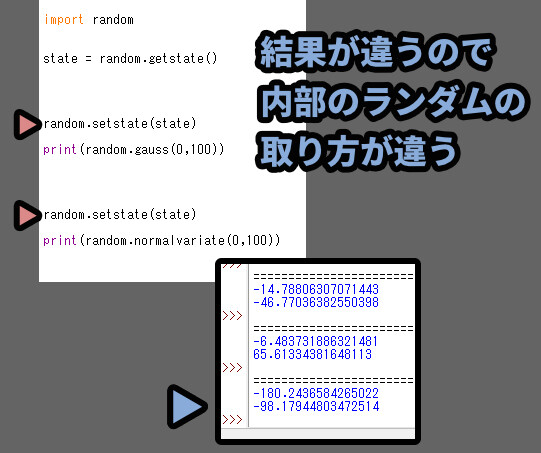
処理的には「gauss」の方が若干、早く動くらしいです。
なので「normalvariate」は基本は使わないと思います。

考え方が違う、2つの正規分布を混ぜて使いたい時向け。
……果たして、そんな場面が来るのだろうか?
以上が、正規分布についての解説です。
フォン・ミーゼス分布
円の角度上で分散を考える上で使われる分布です。
天体界隈で使う… らしい。
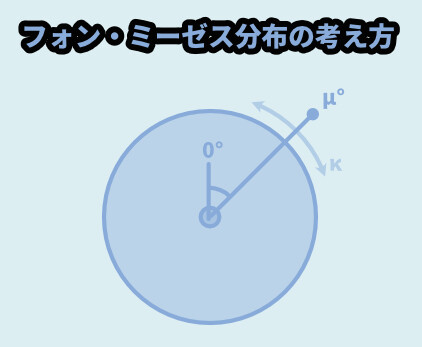
(μ / ミュー)と(κ / カッパ)の2つの要素で形を作ります。
random.vonmisesvariate(μ, κ)
・μ → 初期値の角度(単位はラジアン)
・κ → 拡散率これを使うと、下図のような分散になります。
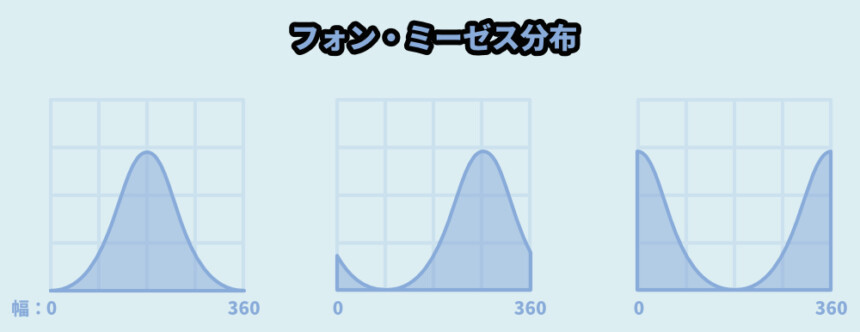
下側で角度を操作すると…
要するに、正規分布ということが分かります。
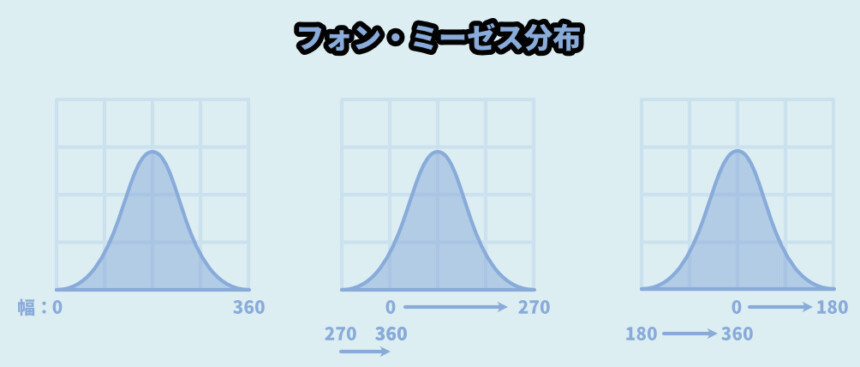
そしたら、こちらを入力すると行きたいですが…
そのままだと「私たちが思ってる感じ」にはならないです。
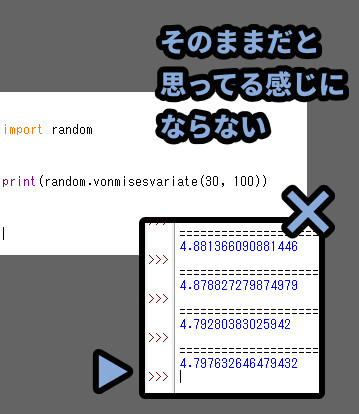
.vonmisesvariate()の角度表示は「rad(ラジアン)」という角度で表記されてます。
私たちが思ってる「° / 度」ではないです。
↓角度の変換はこちらで試せます。


「1rad = 57.2958~ °」らしいです。
なんなんだ、この単位は…。
そしたら、先ほどの処理を確認。
下記の2点で、よくわからない感じになってました。
①角度の単位をradで入れる場所に°を入れてるミスをしている
②結果がrad角で帰ってくることに気づいてない
ちょっとradは使いにくいので… 「radを°に変換」する処理を入れます。
変換処理は「math」というモジュールを入れることで作れます。
import random
import math
print(math.degrees(random.vonmisesvariate(math.radians(30),100)))・math.degrees() → rad角を°に変換する処理(②)
・math.radians() → °角をradに変換する処理(①)

これで、結果が分かりやすくなったと思います。
以上が、フォン・ミーゼス分布です。
対数正規分布
ちょっと変形が入った正規分布です。
大きい数字が出やすい正規分布と考えてください。
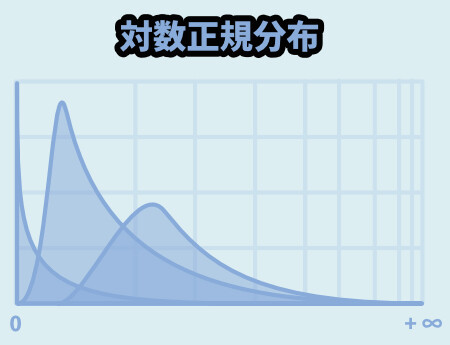
対数表示でグラフを書くと、元ネタが正規分布ということが分かります。
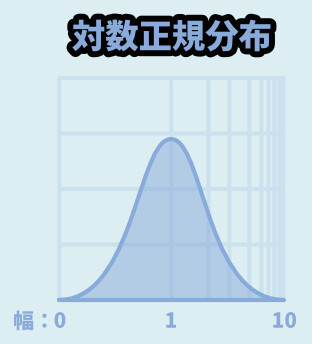
パラメーターはガウス分布などと同じ、μとσです。
random.lognormvariate(μ,σ)
・μ → 初期値ズレ
・σ → 拡散率対数なので、σ = 5でも大きな数字が出ます。
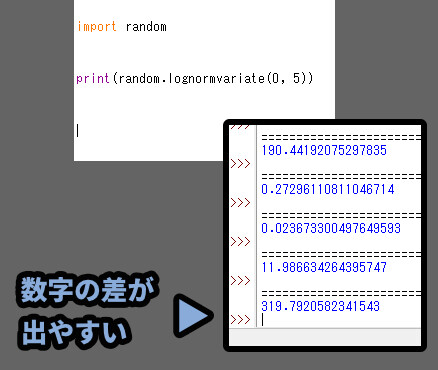
以上が、対数正規分布です。
べき分布系
多くの人が持ってる特性などに使われる分布です。
ロングテールなどと呼ばれたりします。
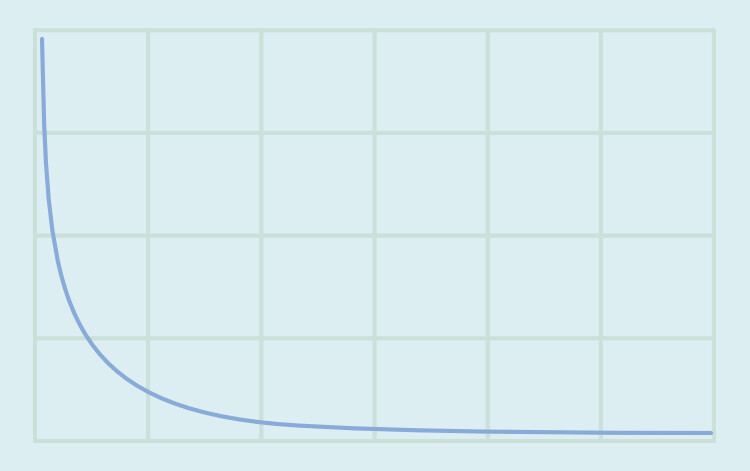
特徴は、べき分布は「平均と中央値」がズレる事です。

・平均値 → すべての数値を足してから、足した"数"を割る
(100人いたら、全部の値を足して÷100した値)
・中央値 → 全ての人の値を並べて、足した数÷2の人の値を取る
(100人いたら値が50番人目の人が持つ値)
「べき分布」で代表的なのが “年収” です。
平均値だと、億万長者が平均を吊り上げるので…
中央値の方が実態を表してるとされてます。
例:2023年の年収(詳細)
・平均値 → 414万円
・中央値 → 360万円
そしたら、このベキ分布っぽい形になるモノを紹介していきます。
指数分布
指数分布は “べき分布” っぽい形になります。
Pythonのrandom場合… パラメーターは「λ / ラムダ」だけです。
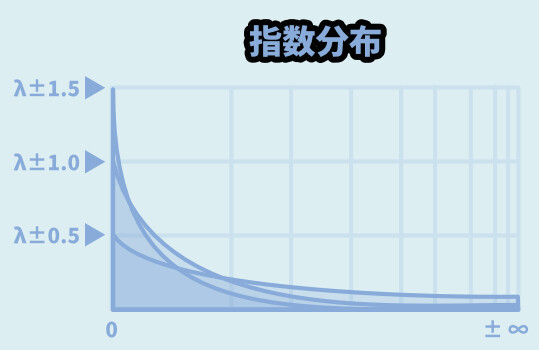
random.expovariate(λ)
λ = 値が小さいほど、大きな数字まで出るようになるλ = 10だと、0に近い数字が安定して出ます。
λ は「-」にしたり、小数点以下を入れてたりします。
試しに「λ = -0.001」にすると、結果の値が「-」になります。
そして、λ値が小さいので、大きな数字が出やすくなります。

以上が、指数分布の解説です。
パレート分布(べき分布)
パレート分布も同じく、べき分布を表します。
指数分布と、若干カーブの形が違うようです。(詳細)
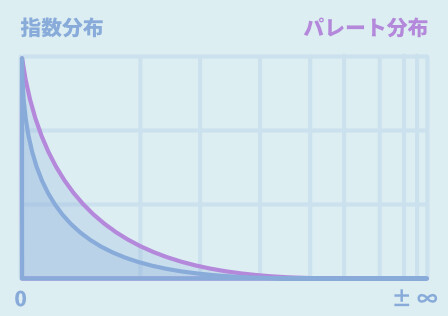
ここでは、べき分布 = パレート分布という扱いで進めます。
(Pythonのrandomに、”べき分布” 専用の設定が無かったので)

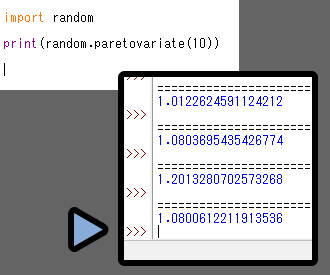
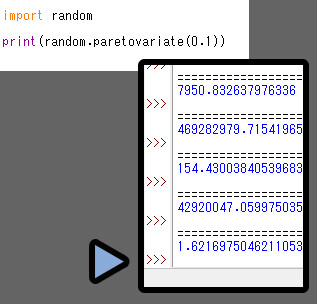
これは、random.paretovariate(α)で表します。
α = 分散率。
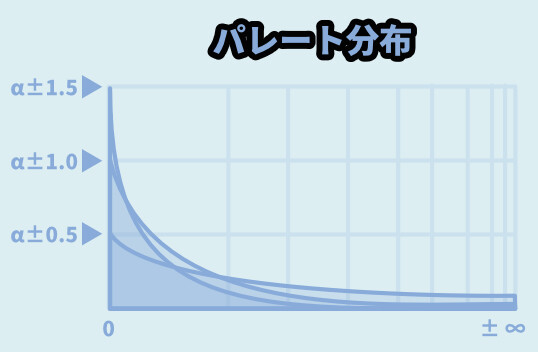
α値が大きいと、小さい数字で安定しやすいです。
α値が小さいと、大きな値まで出るようになります。
以上がパレート分布です。
その他の分布
一様、正規、べき以外の形になる分布を紹介します。
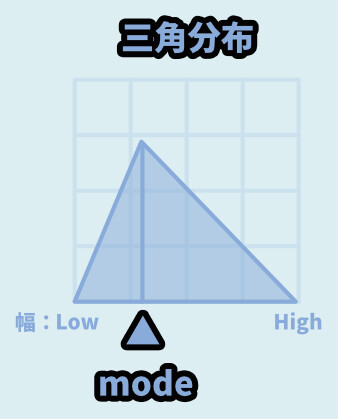
三角分布
三角分布は、三角形の分布になります。
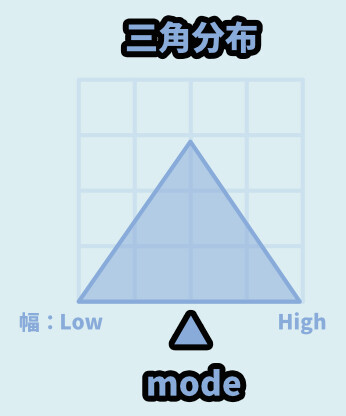
パラメーターは下記の3つ。
random.triangular(最小値, 最大値, 軸になる値)
・最小値 → Low
・最大値 → High
・軸になる値 → modoこの3つを使った、ランダム値を生成できます。
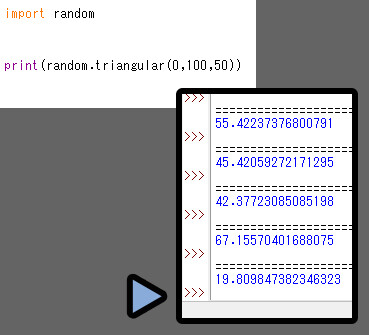
modoを触ると、値の軸が変わります。
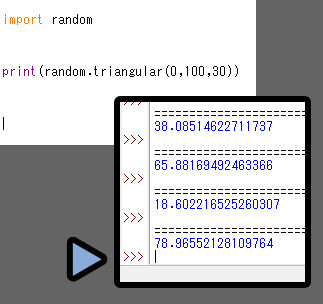
mode = 30にすると… 30に近い値が出てるようですが…
正直、体感として違いは分かりにくいぐらいです。
そしてバグなのか… modo値は「Low」と「High」を超えた値に設定できます。
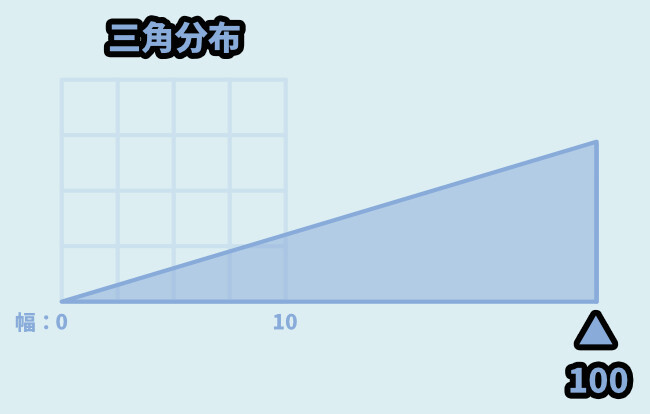
詳細はよくわかりませんが… 謎の値が出ます。


怪しい挙動なので、使わない事をおすすめします。
以上が、三角分布です。
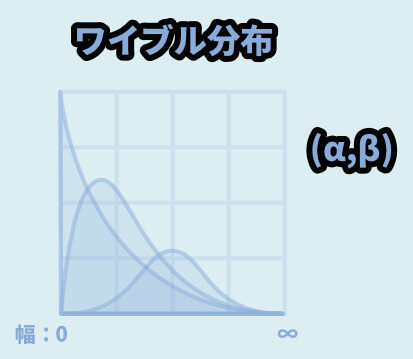
ワイブル分布
αとβの2要素で様々な形を作れる分布です。
主に「機械の壊れやすさ、壊れる確率」を表すのに使われるモノとされてます。
α = 0.1 / β = 5だとベキ分布っぽい形になります。
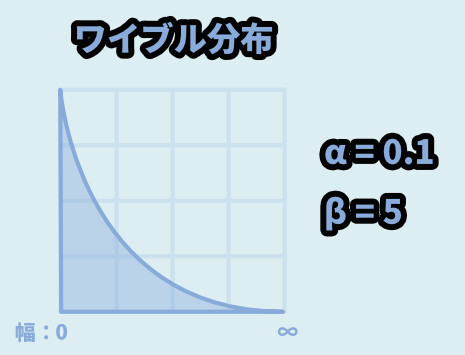
下図のような挙動です。
α = 5 / β = 1だと正規分布っぽい形になります。
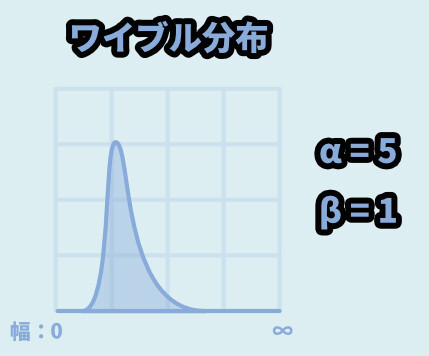
下図のような挙動です。

α = 5 / β = 5だとより、正規分布っぽい形になります。
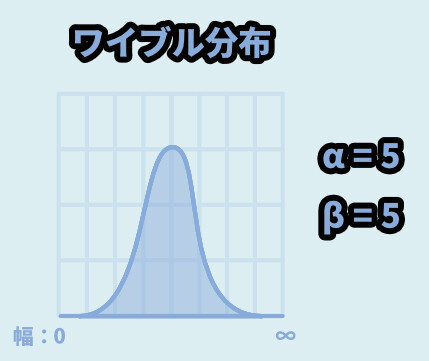
下図のような挙動です。

機械設計に関わる人は使う… のかなぁ…? という一品。
以上が、ワイブル分布です。
ベータ分布
αとβの組み合わせで様々な形が作れる分布です。
値の範囲は「0~1」と決まっており、間は小数で出る形になります。
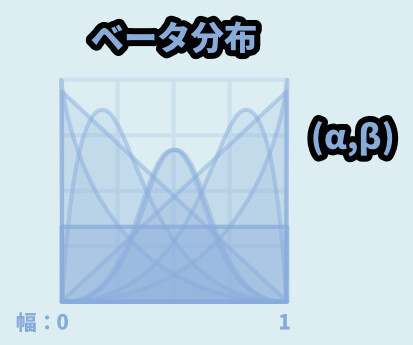
使い道は… 正直、不明。

要素が複雑すぎるので、人間には扱えない感…。
エンジニアのおもちゃ的なモノになるぐらい…?
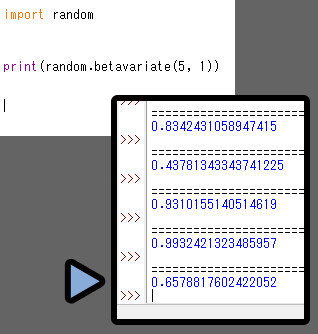
α = 5 / β = 1だと、1に偏ったべき分布みたいになります。
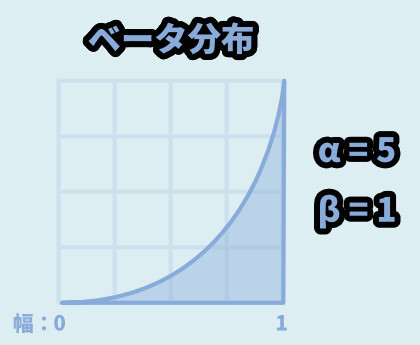
挙動は、下図の通り。
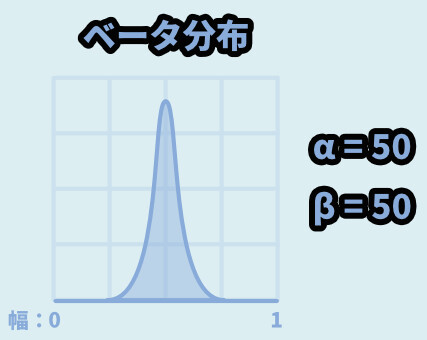
α = 50 / β = 50だと尖った正規分布っぽい形になります。
挙動は下図の通り。
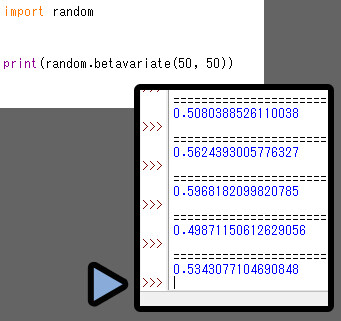
以上が、ベータ分布です。
おまけ:Classを使った書き方
class random.Random() という形で、ランダムを書く事ができます。

俗にいう、オブジェクト指向と呼ばれる書き方だと思います。
class部分には、任意の変数を入れます。
そして、変数名.実行したい処理()と書くと楽だよね? というモノです。

これでrandomの文字を「r」の1文字に省略できたりします。
それ以降の.~~~~()はこれまで紹介した通りのモノが使えます。
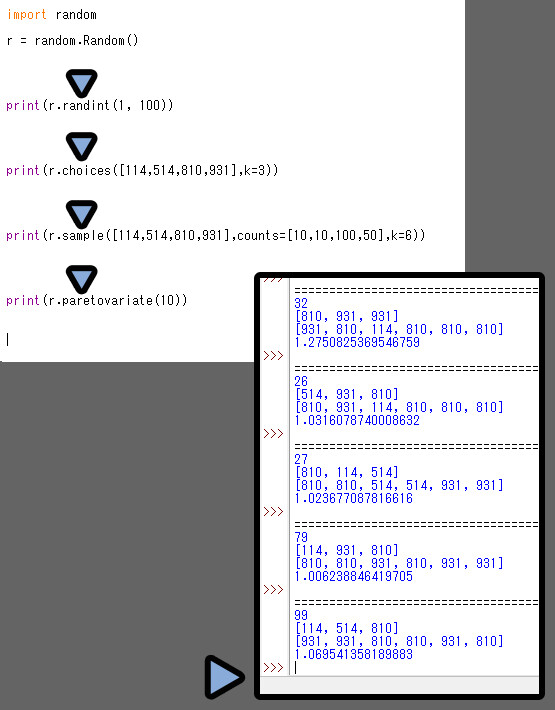
以上が、Classを使った書き方です。
まとめ
今回は、Python付属のrandomモジュールの使い方について解説しました。
・ランダムは疑似乱数という、複雑な数字を使って表現している
・データは整数、小数、文字、リストなどが扱える
・SEED値を決めると、疑似乱数の状態を固定できる
・get/set stateで疑似乱数の状態をリセットできる
・カウスやパレート分布を使えば、値の出方を変えれる
また、他にもPythonやプログラムについて解説してます。
ぜひ、こちらもご覧ください。


コメント