はじめに
今回はノーマルマップについて解説します。
前提として面法線と頂点法線の違いの知識がある事を想定して進めます。
こちらの記事を見た上で読み進めてください。
法線マップの画像
法線マップの画像はこのような紫色のサイコパスな色合いで凹凸が表現されます。

これはモノクロ画像を変換して作ることができます。
暗い場所は凹み、明るい場所が膨らみとして変換されます。


作り方はKritaの場合はフィルターマスク、Unityの場合はノーマルマップ設定でできます。
法線マップの正体
まず面には面法線があり面の向きが決まります。

次に、頂点には頂点法線があり大きな明暗の向きが決まります。

そして法線マップがあります。
これは面法線をピクセルで分割して画像で向きを表してます。

これを割り当てることで頂点法線で決まった明暗に変化をつけることができます。

画像なので180度を超える事はありません。
なので頂点法線の方が明暗に与える影響が大きいです。
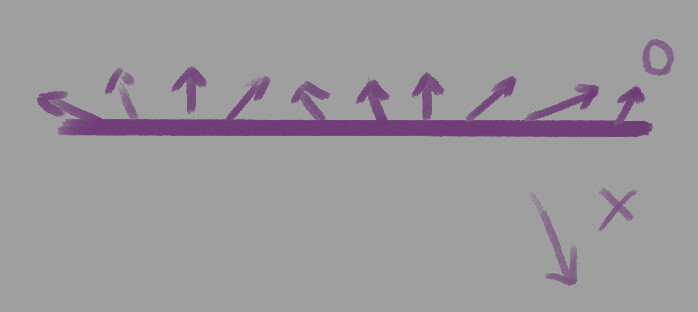
スムースシェードをかけた頂点法線とその時の陰影のイメージ図です。
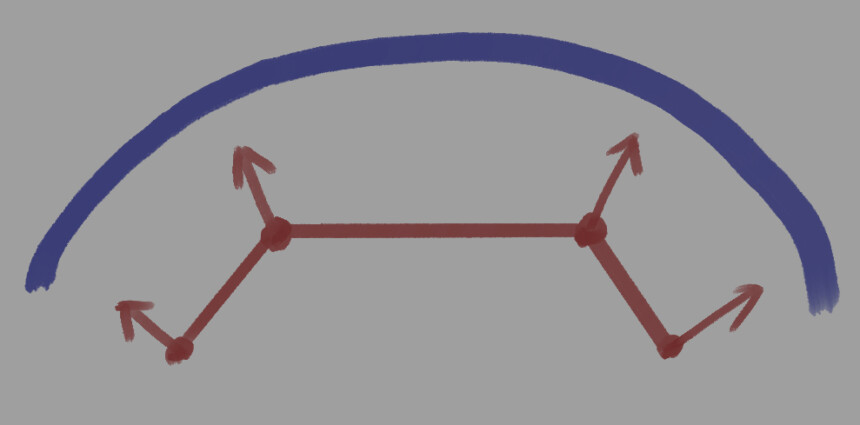
これにノーマルマップを割り当てます。
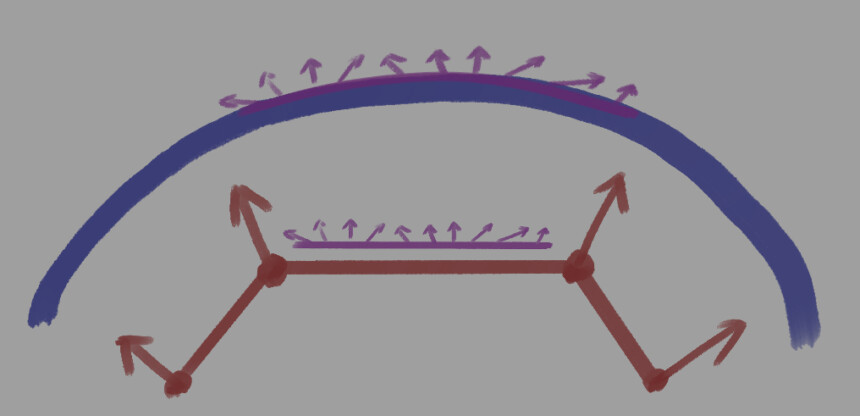
すると頂点法線による明暗を元に法線マップが補助的に明暗の情報を付与します。
これが法線マップの正体です。
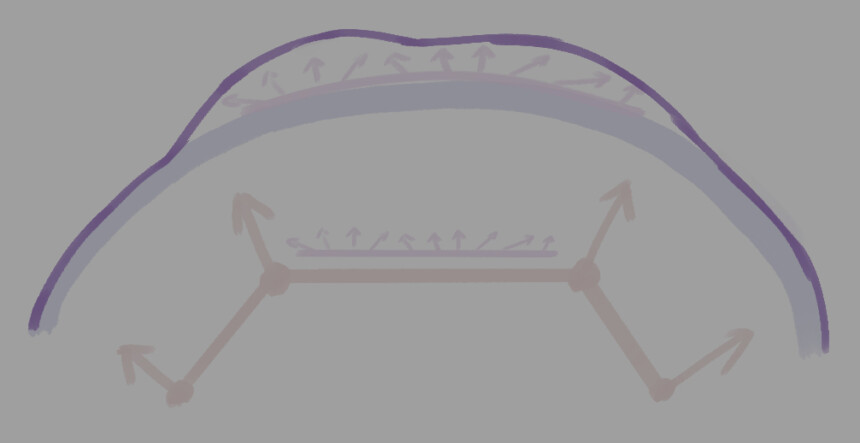
頂点法線が反転した所でのノーマルマップの挙動
理解を深めるために、頂点法線が反転した所でのノーマルマップの挙動を考えます。
頂点法線が反転した所ではノーマルマップはある地点を境に凹凸が逆になり表示されます。

図面での説明
まずこのような頂点シェードが1か所だけ反転した面を用意します。
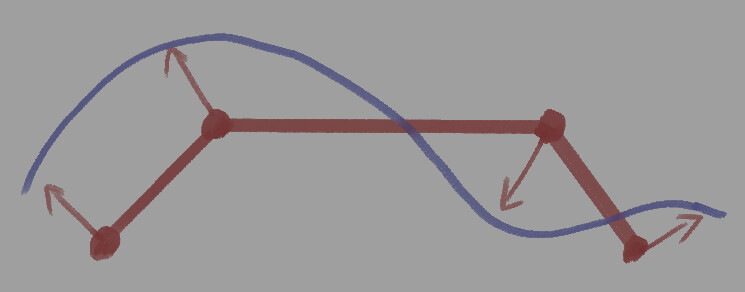
すると、ある地点で明暗の向きが反転します。
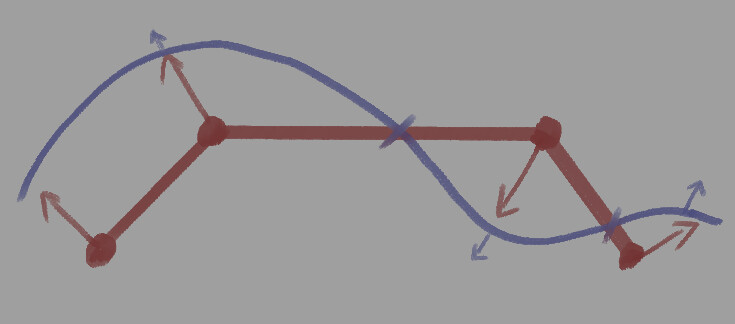
この上にノーマルマップを置きます。
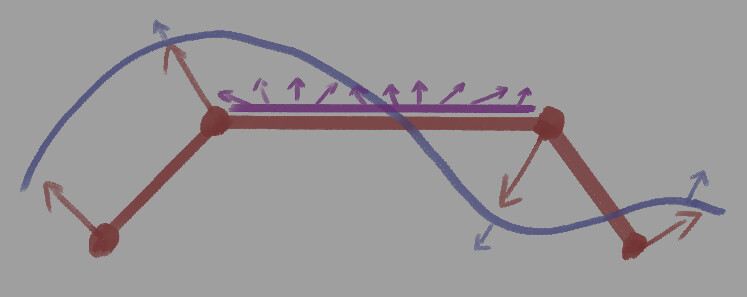
するとこのように割り当てられます。
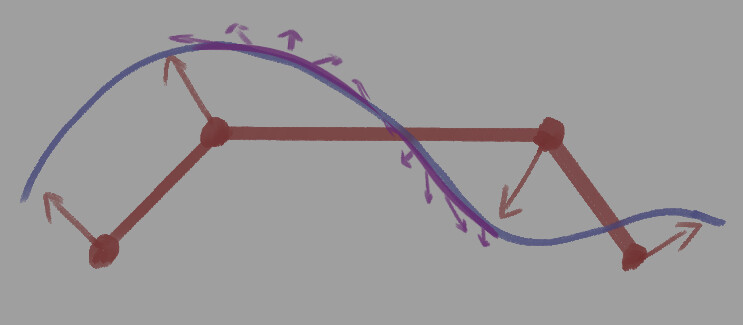
頂点法線によって決められた大まかな明暗の上に法線マップの情報が乗ります。
法線マップ自体には大きな明暗をする力がありません。
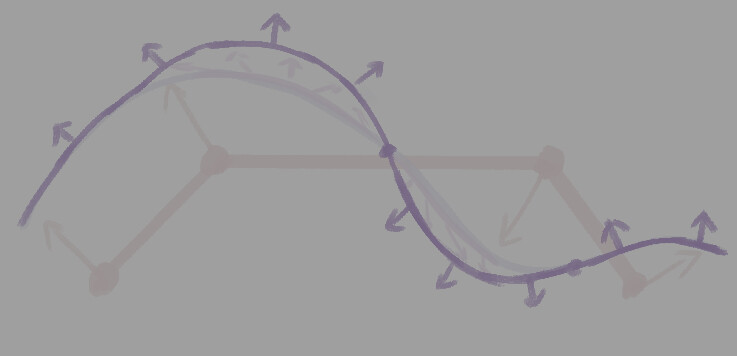
頂点法線が反転した所でのノーマルマップの挙動
Blenderでの実験
これをBlenderで表現するとこのようになります。
頂点法線を編集して一部の明暗を反転させた状態です。
ある地点を境に明暗が反転して暗くなってる事が確認できます。
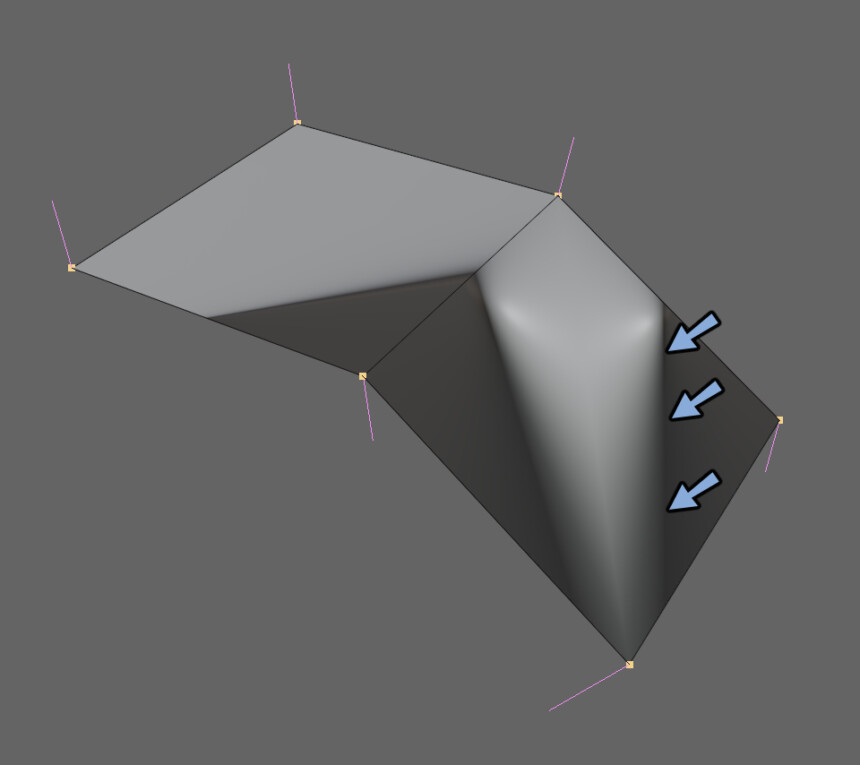
この上から法線マップで面に細かな凹凸の明暗情報を割り当てます。
するとこのような挙動になります。
暗くなっていた所の凹凸の表現が逆方向になったことが確認できます。

反転する位置の決まり方
これは以下の2つで決まります。
・4角面の3角面解釈問題
・その三角面が持つ頂点法線の情報
実験の為にKキーでナイフツールを起動。

4角面にはこの2パターンの3角面の解釈ができます。
そして4角面はPCが一度3角面に変換して明暗を処理しています。
面を分割することで解釈方向を固定できます。

これで明暗の挙動が変わります。

左側の3角面はどれも反転した頂点法線です。
なので途中で明暗のねじれが面の変わり目に近い位置にあります。

右側の3角面は1か所反転しなかった頂点があります。
なので大きく斜め線が入り明暗がねじれてます。

これで解釈された3角面とその面が持つ頂点法線の情報が反転する位置を決めてる事が分かりました。
まとめ
今回はノーマルマップを使う上で必要となる知識と仕組について解説しました。
・グレースケールの画像を変換して作ることができる
・大きな明暗は頂点法線で制御
・細かな明暗は法線マップで作る。
これらの知識を活かして3DCGの製作にお役立てください。
ーーーーー
またノーマルマップ関連でよく起こりそうなエラーや法線の設定方法はこちらで解説しています。
面法線の設定方法
頂点法線の設定方法
ぜひこちらもご覧ください。









コメント