はじめに
今回は、作品制作に役立つ “花” 全般の構造について紹介します。
植物学の記事では無く… このような花モチーフの作品を作るために役立つ知識のまとめです。


葉や植物全体の事などは「おまけ」で少し触れますが…
この記事では、細かくは解説しません。
(他の人の記事がクォリティが高かったので、それをおすすめ記事として載せてます。)
花形(かけい)
花形 = 花びらの付き方です。
下記のような区分に分けられます。
・放射相称
・螺旋入り放射相称
・左右対称
・非相称花【放射相称】
一般的な花の形です。
1つの点(中央)を元に放射状に花びらが付きます。
※5枚の花びらの場合、5放射相称など呼ばれます。

【螺旋入り放射相称】
中央の1点から、大きさを変えて螺旋を描くように花びらが着く形です。

この螺旋放射相称の角度は多くの場合で137.5°になります。
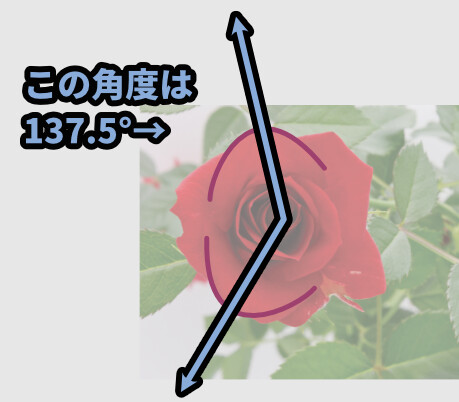

137.5°は “黄金角” と呼ばれる角度です。
詳細は後ほど紹介します。
【左右対称花】
文字通り左右対称の花です。
マメ科植物の花などに見られます。

【非相称花】
これまで紹介したような法則性が当てはまらない花です。
ヤブヅルアズキなどがこの形になります。

以上が花形です。
黄金角のらせん構造
黄金角=137.5度。
これは薔薇の花びらの生え方など、自然物の多くの形で確認できます。


植物の専門家からは怒られますが…
クリエイター的には、植物系の造形で資料不足で困った時は
だいたいこれを採用するとなんとかなるという角度です。
この黄金角の由来を知るにはまず「フェボナッチ数列」を理解する必要があります。
フェボナッチ数列は1+1からスタートし、「答え」と「足し算に使った前の数字」を足していく数列です。
(図を見た方が早いと思います)

そして、フェボナッチ数列で使った数で割り算をすると 「1.618…」のような数字になります。
この数字を使った比率「1:1.618」が黄金比です。

そして、円の角度を黄金比で分けたモノの小さい方が黄金角です。
【黄金角の計算】
円 = 360°
360 ÷ 1.618 ≒ 222.5
360 - 222.5 = 137.5
ーーーーーー
【コレで下記のことが成り立つ】
222.5 + 137.5 = 360°(円)
1:1.618 = 137.5:222.5薔薇などの螺旋入り放射相称の花などはこの角度が使われることが多いです。

ただ、自然のモノなので形には誤差の揺らぎがあります。
なので完璧な137.5°は自然界では少ないです。
なので、137.5°に近い数字で収まるぐらい考えてください。

ちなみに、こちらのサイトではより詳しく解説されています。
他の黄金角と性質が近い角度の例や、動かしてみて間隔的に分かるプログラムが用意されてます。
↓おすすめです。
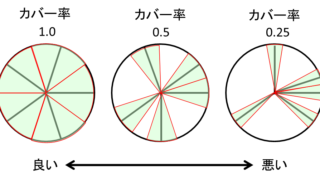

黄金角を採用すれば、だいたい何とかなりますが…
もちろん、例外があります。
なので、実物の観察と測量が大切。
その上で、例外を見つけた時はこの考え方を思い出してください。
以上が、黄金角の螺旋構造の解説です。
花序と葉序
花と葉っぱには付き方の法則があります。これが「花序(かじょ)」と「葉序(ようじょ)」です。
↓こちらはその例の一部。
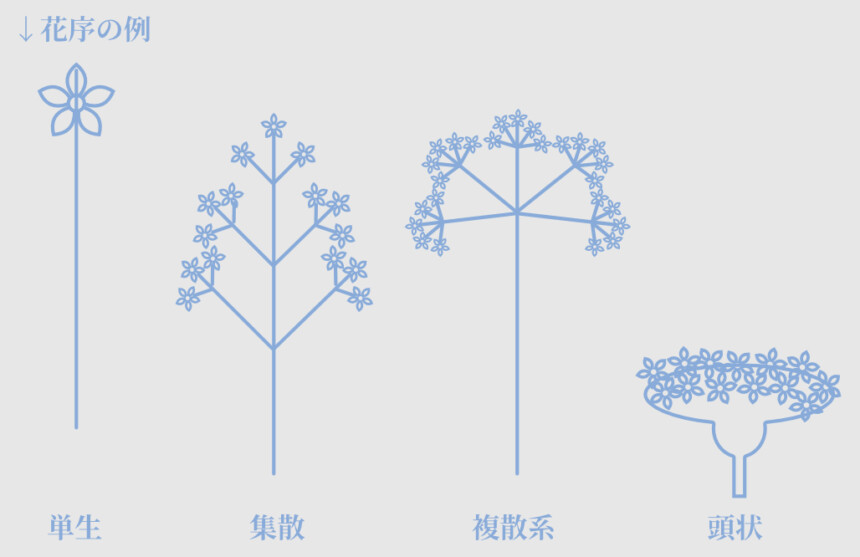
数が多いので、ここで全ての形の解説は省きます。
詳細はコチラなどをご覧ください。

種類が多いので、全部覚えようとせず。
「作りたい植物の名前」+「花序」や「葉序」で調べた方が早いと思います。
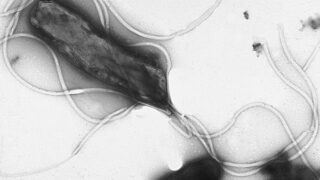
舌状花と管状花
花には2種類の花が合わさったモノがあります。
主にキク科の植物でこの形が出てきます。
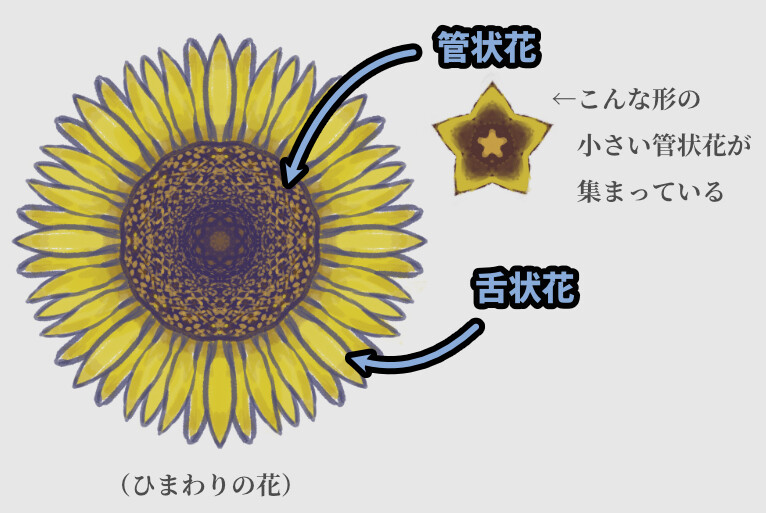
中には「舌状花」を捨て「管状花」だけになったモノがあります。
コセンタングサがその例です。

コセンタング/ アイノコセンタングサ / シロバナセンタングサを見るとこの舌状花を失う過程が分かりやすく観察できます。

以上が、舌状花と管状花の解説です。
包葉
ブーゲンビリアの花などは、そのまわりを包むように変形した特殊な葉があります。

この葉っぱを「包(ほう)」や「包葉(ほうよう)」と呼びます。
花の原形は “葉”
花はどこから来たのか。
その答えは “葉” です。
では、どうやったら葉が花になるのか?
これを理解するのに役立つのが、次紹介する「ABCモデル」です。
八重咲の仕組み (遺伝子欠損/ABCモデル)
葉の遺伝子に「A,B,C」の3つの要素があると考えられてます。
この3つの組み合わさり形で、葉が花びら、おしべ、めしべ、ガクなどになると考えられてます。
そして、AとCは抑制関係で組み合わせれないという設定です。
なので、ABCの3つの遺伝子から、下記の7通りのパターンができます。
・すべてなし = 葉
・Aのみ = ガク
・Bのみ = 花びら or おしべ
・Cのみ = めしべ
・A+B = 花びら
・A+C → 組み合わせる事ができない(抑制関係)
・B+C = おしべこの3つの遺伝子が正しく入っていれば、普通の花ができます。

そして、1部でも欠損すると特定のパーツが作られなくなります。

【A欠損の場合】
・すべてなし = 葉
・Cのみ = めしべ
・B+C = おしべ
→ 「ガク」と「花びら」が消える
AとCは抑制関係で、片側が消えるとその分を残った方がカバーします。
A以外の、他の遺伝子も欠けます。
【B欠損の場合】
・すべてなし = 葉
・Aのみ = ガク
・Cのみ = めしべ
・A+C → 組み合わせる事ができない(抑制関係)
→ 「花びら」と「おしべ」が消えるそして、多くの場合の八重咲はC欠損です。

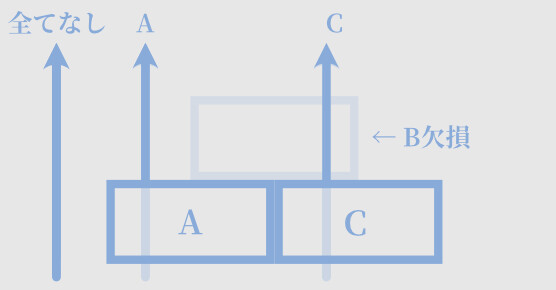
【C欠損の場合】
・すべてなし = 葉
・Aのみ = ガク
・A+B = 花びら
→ 「めしべ」と「おしべ」が消える
→ 結果、めしべが花びらに置き変わったような形になる(これが八重咲き)あと、2つの遺伝子が欠損することもあります。
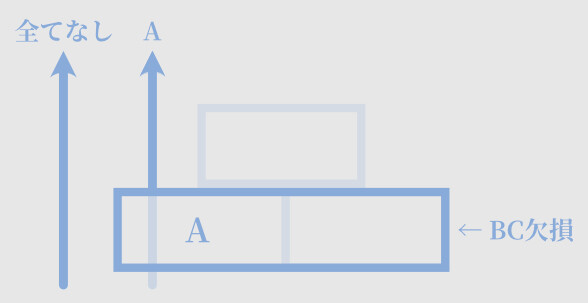
【BC欠損の場合】
・すべてなし = 葉
・Aのみ = ガク
→ 「ガク」と「葉」だけになる
2つ以上の欠損は、繁殖に問題が出てくるので滅多に見かけません。

【AC欠損の場合】
・すべてなし = 葉
・Bのみ = 花びら or おしべ
→「めしべ」と「ガク」が消える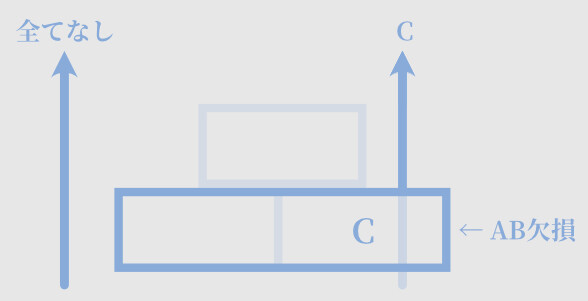
【AB欠損の場合】
・すべてなし = 葉
・Cのみ = めしべ
→ 「葉」と「めしべ」だけになるそして、ABC全てが欠ける事パターンも考えれます。

【ABB欠損の場合】
・すべてなし = 葉
→ 「葉」だけになる
ちなみに、花を咲かせるのに必要な栄養が不足していると…
遺伝子に問題が無くても花が咲かない事があります。
花が咲かないモノの場合、栄養不足の可能性があるので注意。
以上が、ABCモデルと八重咲きの仕組みの解説です。
(八重咲きの花を作る際、めしべを作らないように注意)
斑入り
多くの植物は、遺伝子の欠損やウイルス感染が起こると枯れて死にます。
が、たまにその中で生き残るモノも居ます。
このような「遺伝子欠損」や「ウイルス感染」に耐え、色などの情報が欠けたり状態で生存するようになると “斑入り” になります。

オシロイバナなどで確認できます。
以上が、斑入りの解説です。
帯化
植物の成長点で(頂端分裂組織)に異常が起こって発生する形です。
ケイトウは、この帯化で遺伝子が固定化されました。


作画は基本しないと思いますが…
こういうモノもありますという紹介。
おまけ:葉 – より植物について知りたい人へ
最後に、その他の植物に関する言葉とおすすめの参考記事を紹介します。
【草姿(ようし)】
植物全体の形です。
【葉身】
葉の中から葉柄を除いた部分です。
【葉脈 / 花脈】
植物には水や養分を運ぶ人間でいう "血管" があります。
これの、葉っぱにあるモノが葉脈(ようみゃく)花にあるモノが花脈(かみゃく)です。
【葉縁(ようえん)】
葉のフチの形です。
花のフチの言葉は無かったですが… 同じような考え方ができると思います。これらの言葉の詳細は↓こちらの解説が非常に分かりやすいです。

私の方で記事をまとめても、似たような図と解説にしかならないと思うのでリンクで紹介。
まとめ
今回はクリエイター向けに、作品制作に役立つ”モノ”全般の構造について紹介しました。
・花形(かけい)は花びらの付き方
・花形は「放射相称 ・螺旋入り放射相称 ・左右対称 ・非相称花」などがある
・花びらの原形は葉
・葉が花びらになるには3つの遺伝子が関わっている
・3つの遺伝子の「ABCモデル」を学ぶと八重咲などの仕組みが分かる
・八重咲の花にめしべやおしべを付けると形の間違いになる事があるので注意
・花びらみたいな葉、包葉がある
・キク科の花には舌状花と管状花の2つの花が入ってる事がある
また、他にもクリエイター向けの情報を発信してます。


ぜひ、こちらもご覧ください。


コメント