はじめに
今回はカメラの画角とパースペクティブの考え方について紹介します。
ここでは、まず画角を紹介するために「パースペクティブ」から解説します。

結論だけ言うと…
・パースペクティブ = カメラからの距離による画面の歪み
・画角 = 「画面に映る範囲」と「パースペクティブの歪みの量」を変える
画角にパースペクティブの要素が入るので、まずはパースから解説します。
パースペクティブが発生する仕組み
結論だけ言うと、カメラからの距離による画面の歪みです。
これは「近くのモノは大きく、遠くのモノは小さく写る」から始まります。
近くのモノは大きく、遠くのモノは小さく写る
まず、カメラから近いモノは大きく、遠いモノは小さく写ります。
試しに、あなたの目、眼球の前に、自分の左手か右手を持っていてください。
手の甲でなくて良いですが… 丁度↓の本の表紙みたいなポーズです。
そのまま目から手の距離を離します。
すると、手が 映る範囲が減り、手が視野を占める割合が小さくなったことが分かります。
それが、近いモノが大きく、遠いモノは小さく見える現象です。
近くのモノは大きく、遠くのモノは小さく写る//ーーーーー
この内容を3DCGで整理し、表現するとこちらの図のようになります。
まず、カメラがあり、同じ大きなのモノを近くと遠くに置きました。
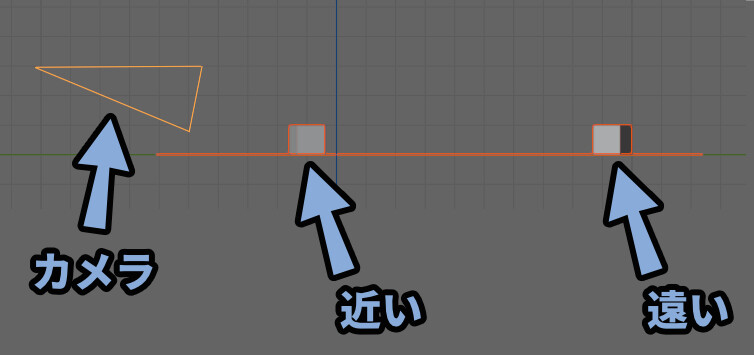
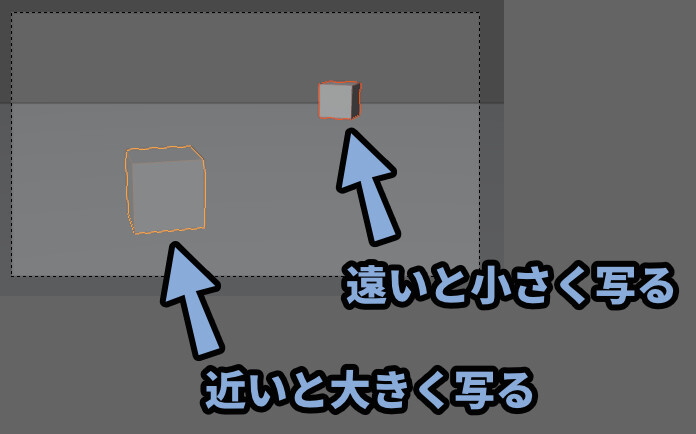
このカメラから見た視点だと、同じ大きさのモノでも距離により画面に小さく写ってます。
並べると、このぐらいの差が生まれてます。
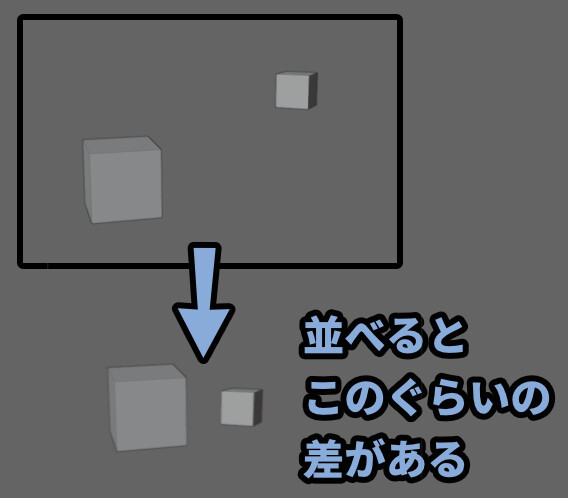
以上が近くのモノは大きく、遠くのモノは小さく写るの説明です。
変化を連続的にすると消失点が発生する
次は2つの棒を用意しました。
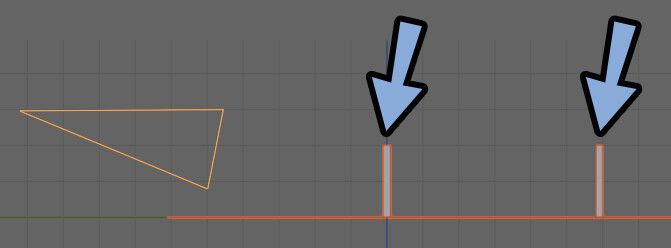
これを並べるとこのようになります。
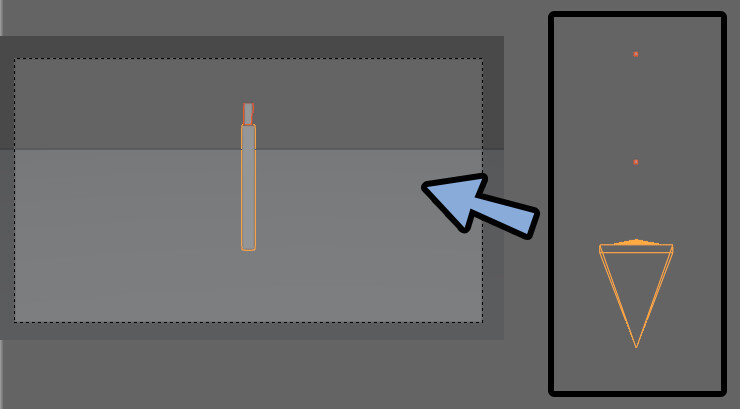
ちょっとわかりにくいので、左側にずらしました。
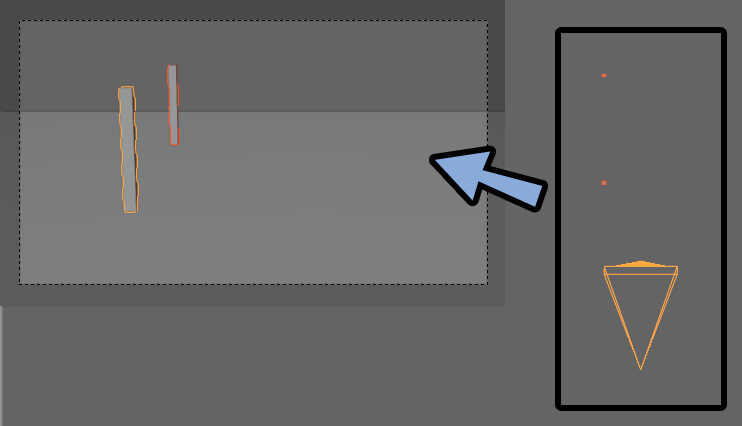
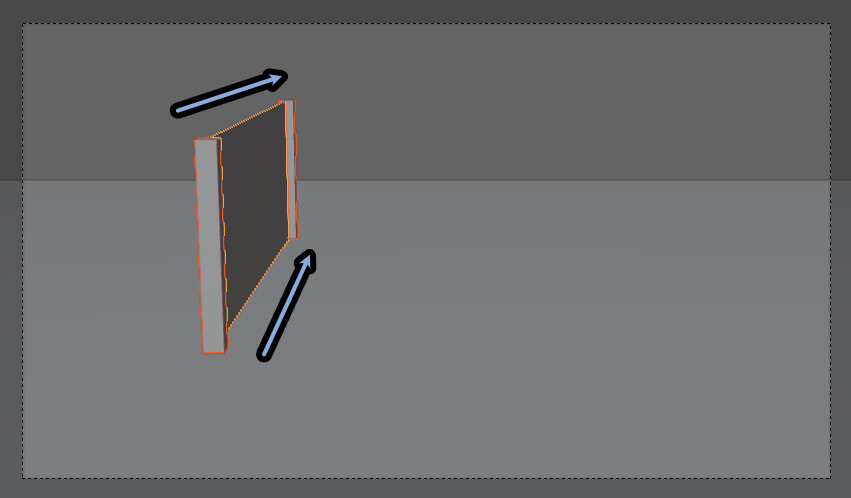
この棒の遠近それぞれの、上下の端を結ぶと…
大きさが連続的に変化してる事が分かります。
この変化を延長していくと… 上と下の端はある1か所にたどり着きます。
これが、消失点です。
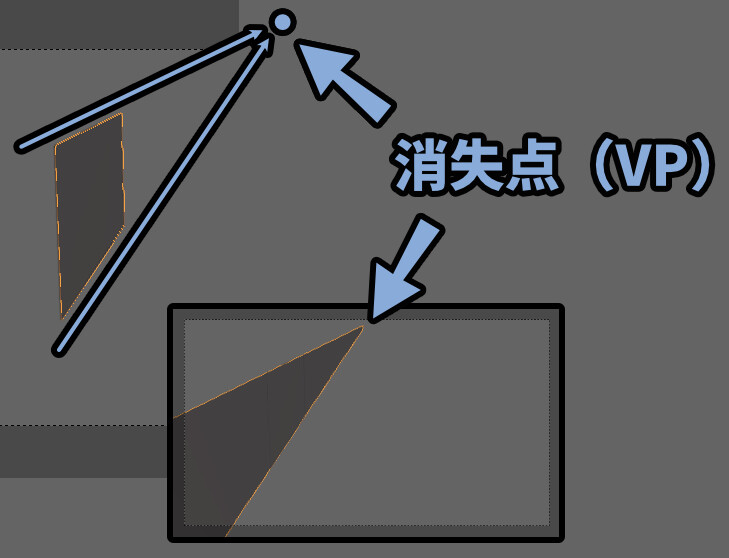
以上が、変化を連続的にすると消失点が発生する事の解説です。
1~3点透視図法
次以降がお絵描き、イラスト界隈でよく言われるパース理論になります。
ちなみに、このパース理論は下記の2つのモノには基本使えません。
・回転して地面に対して平行でなくなったモデル
・立方体や平面以外の角が90度ではないモデルなので、ここから先は角が90度でできた、
地面に対して平行に置かれたモデルを前提とした理論になります。
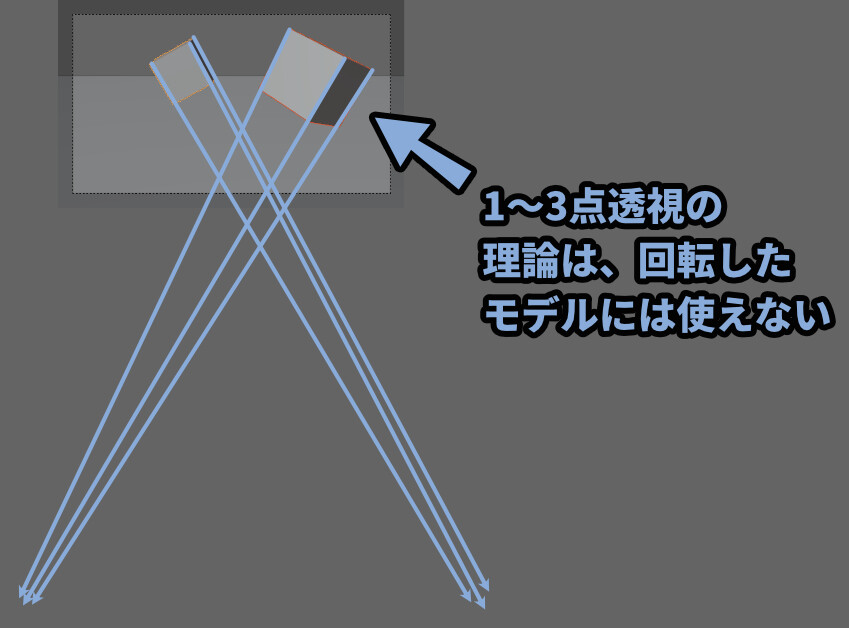
このような地面に対して平行+すべての角が90度のモノにのみ使えます。
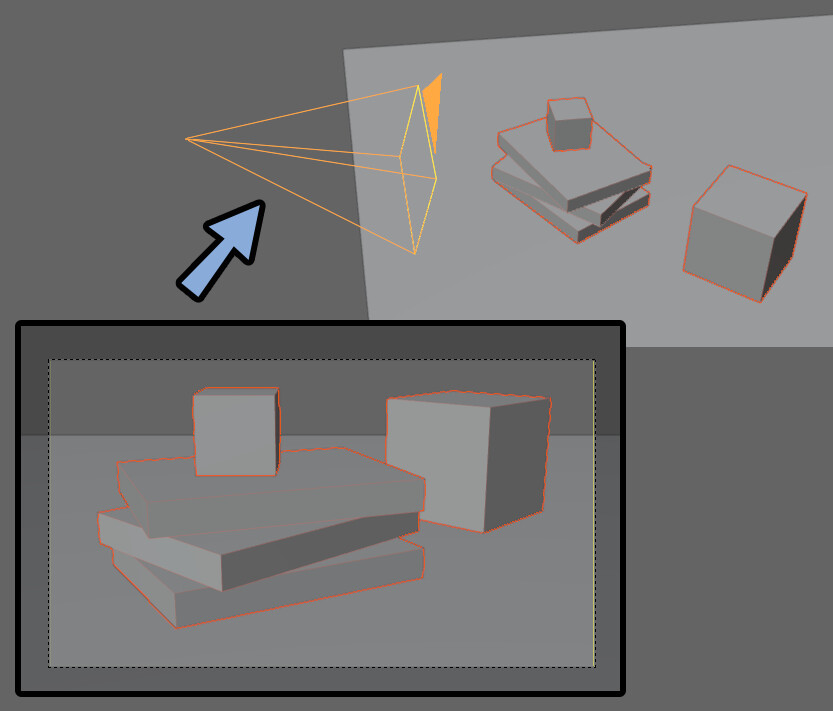

すごい、もはや数学問題レベルの図形処理を頑張れば、
「地面と平行でないモデル」や「角が90°でないモデル」も対応できますが…
シンプルに魔法陣を描くのが面倒です。
なので、個人的には…
美大受験などでアナログで絵を描く必要が無ければこれは覚えなくて良いと思います。
これ覚えるより3DCGの使い方を覚えた方が良いです。
すべての角が90度で交わるようなモノでも…
↓のような地面にガイド線を作成 → ガイド線からアタリを作成 → それを清書より…
3DCGソフト起動して、適用な立方体を作って、それをなぞる方がたぶん早いです。
慣れれば3DCGをイラスト風にもし上げれるので作画効率がこの方が高い(たぶん)。

だいぶ昔の絵描き目指して頃、頑張って勉強しましたが…
3DCGで再現してしまった方が早いし楽という答えに行きつきました。
1点透視図法
これはカメラに対して平行なモノに発生するパース理論です。
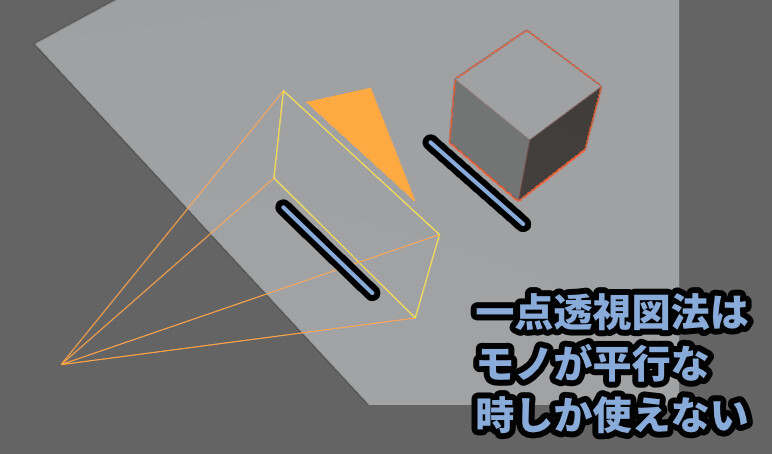
変化のイメージはこんな感じ。
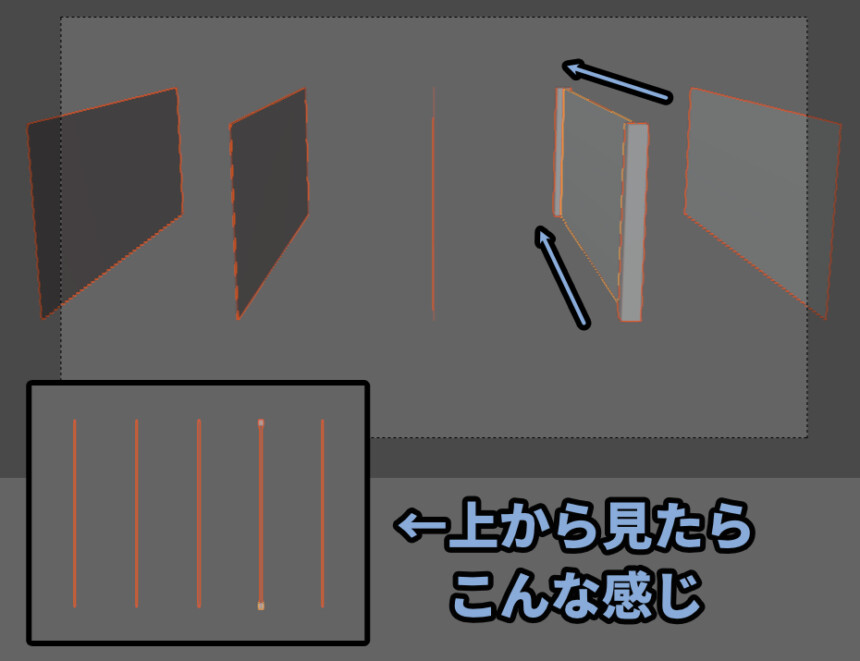
この変化を大きくすると、1か所の消失点にたどり着きます。
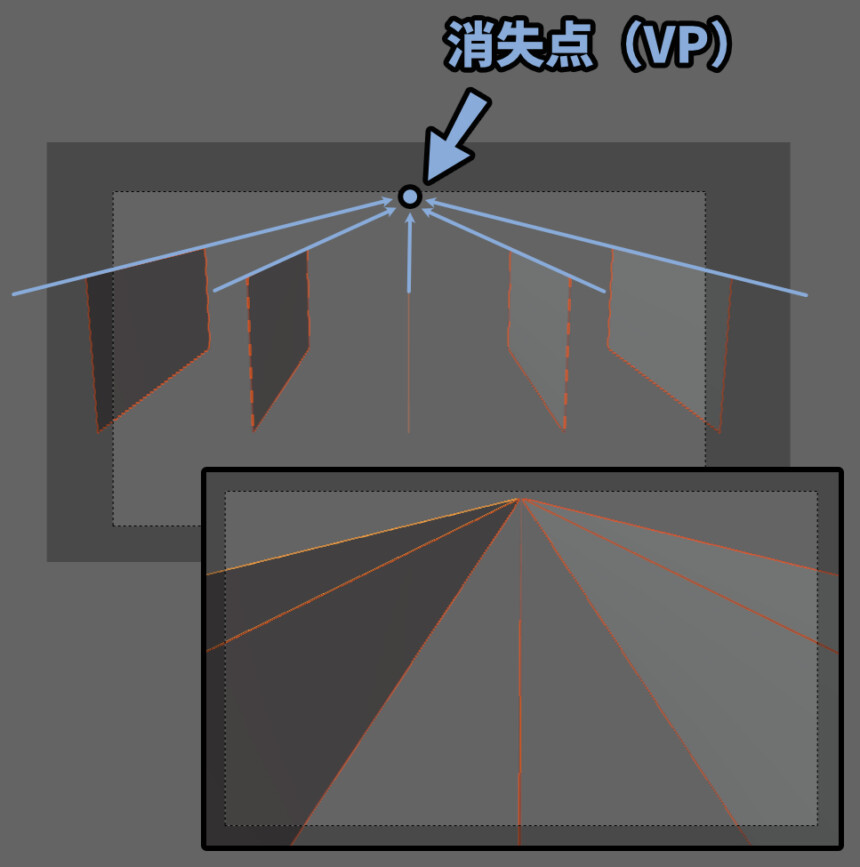
ちなみに、横方向の消失点は基本 “目の高さ” に来ます。
これを「アイレベル(EL)」と言います。
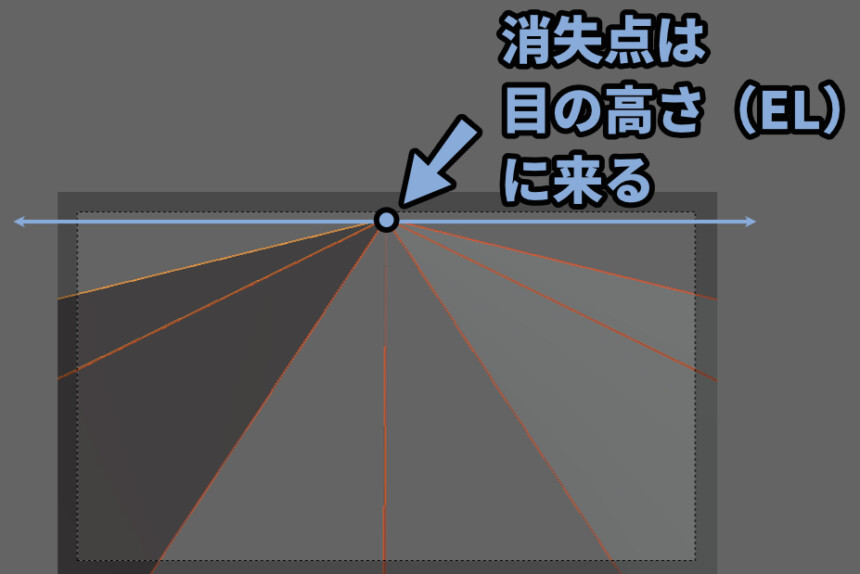
↓の説明が分かりやすいです。(丸投げ)
整理するとこのようになります。
・消失点は1つ(奥行き軸(Z))
・+2つの平行定規を使う(横,縦軸(X,Y))
・横、縦、奥行きの3つの軸が揃ったので三次元的な奥行きを表現できる
→ 結果、遠近感が生まれる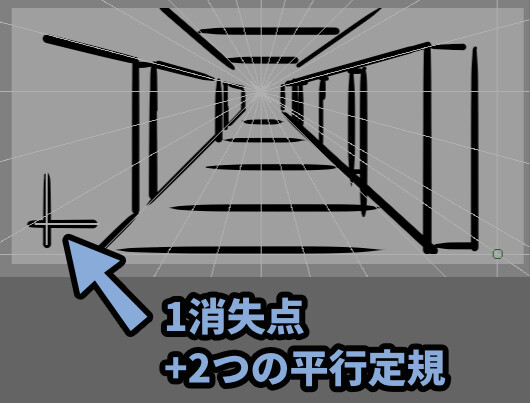
カメラと平行なので、横軸にパースが発生しない。
なので、消失点が発生せず、平行定規を2つ使う事になります。

以上が、1点透視図法です。
2点透視図法
これはカメラに対してモノが回転し、平行では “ない” 時に発生するパース理論です。

↓こんな感じの見え方になります。

何が起こったかというと… 「奥行き(Z = VP1)」と「横向き軸(X = VP2)」が同時に見えてます。そして、2つの消失点が発生しました。
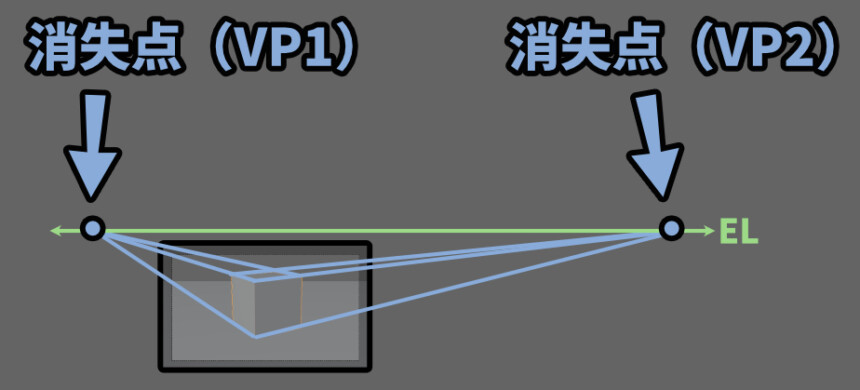

3DCG的な表現を一般の人にもわかるようにしたかったので、「奥行き(Z軸)」と「横向き(X軸)」が同時に見えると書きましたが…
カメラの視点から見て、役割で考えた場合は「奥行き」と「横向き」の軸の “役割が混ざる” と表現した方が分かりやすかったかもしれません。
整理するとこのようになります。
・消失点は2つ(奥行き軸(Z)/ 横向き軸(X))
・+1つの平行定規を使う(縦軸(Y))
・横、縦、奥行きの3つの軸が揃ったので三次元的な奥行きを表現できる
→ 結果、遠近感が生まれる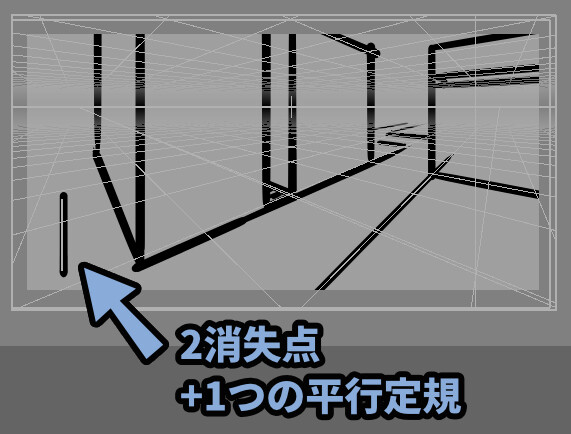
以上が、2点透視図法です。
3点透視図法
これはカメラが上下に回転した時に発生するパース理論です。
先ほど2点透視図法で紹介した作例を、もう一度よく見てください。

画面の端から垂直を取り、立方体の端に当ててみました。
すると… 微妙に角度がついてる事がわかります。
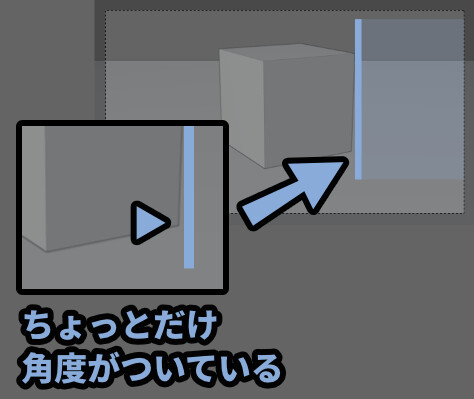
そしてこの変化を辿ると… 3つ目の消失点が見えてきます。
見下ろした場合、下方向に消失点が発生します。
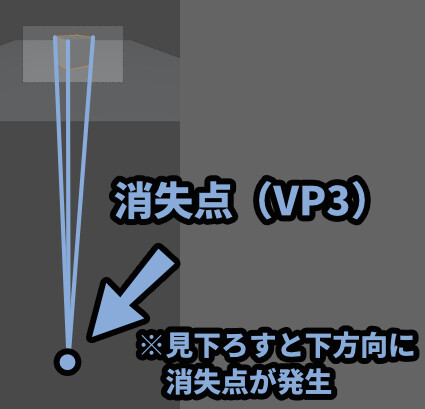
この3つ目の消失点は、上か下かのカメラの回転角度で変化が大きくなります。
ビルなどの高いモノを、地面から見上げて見ると違いがよく分かると思います。
見上げた場合、上方向に消失点が発生します。
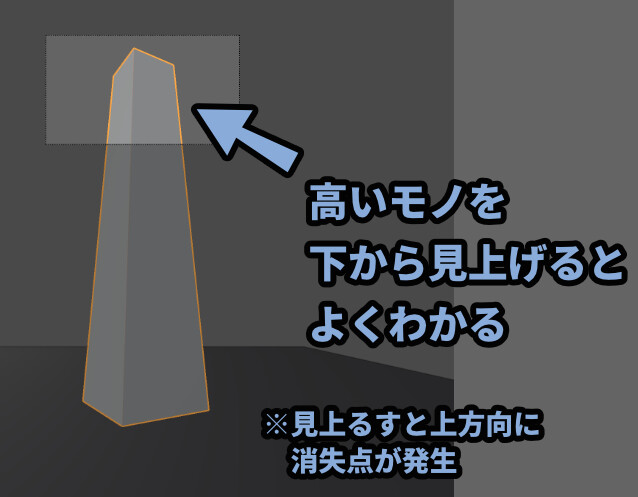
これが、3点透視図法です。
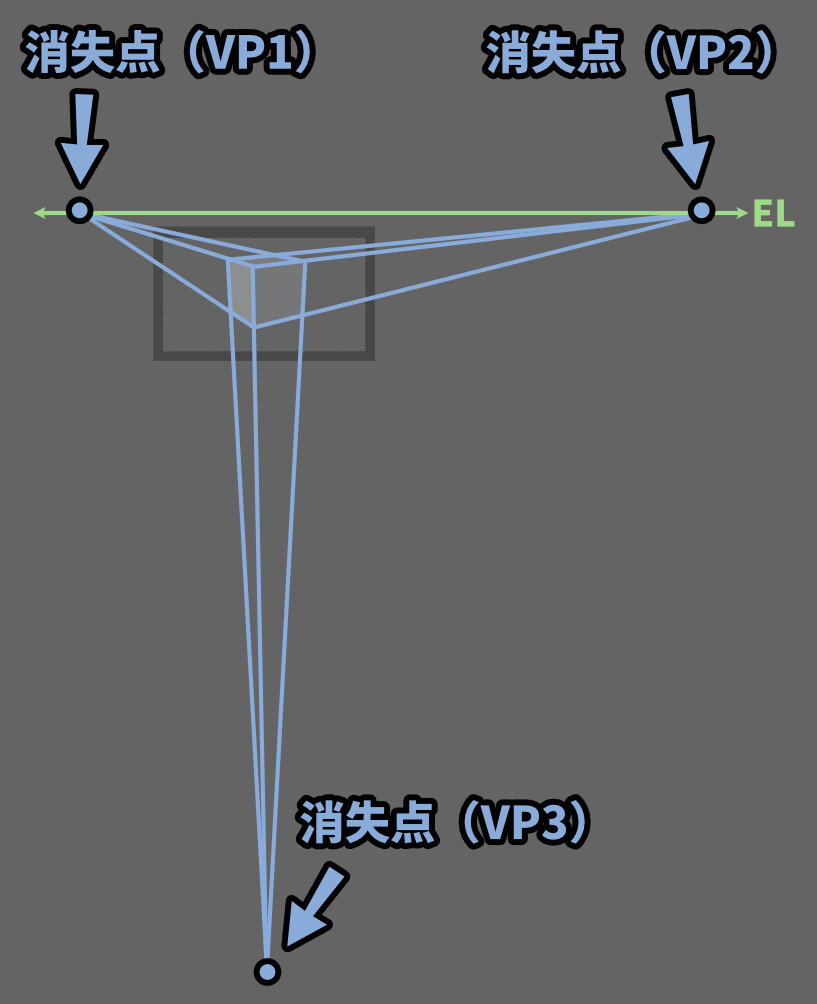
そして、先ほどの作例は、説明のために2点透視図法としましたが…
厳密に言うと3点透視図法です。

この後も、説明のために3点透視図法を2点透視図法と表記してる所があるので注意。

この順番や説明の方が分かりやすいと思い、
若干、嘘の説明を入れてます。ごめんね。
1~3点透視図法の説明が終わったので、次は消失点の行き先について整理します。
横方向の消失点は目の高さに帰結する
カメラを地面と平行にし、モノをたくさん置いて見ました。

このように、モノが複数ある場合…
これらのモノ全てに “消失点” は発生します。
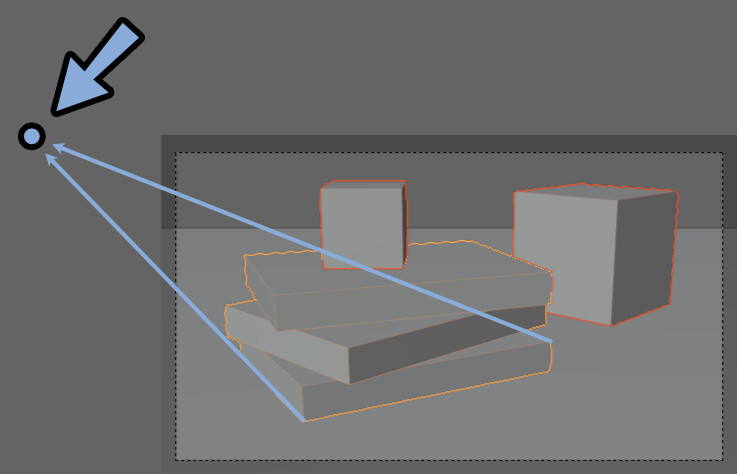
そして、横方向(ZとX軸)のすべての消失点は “EL” の線上に発生します。
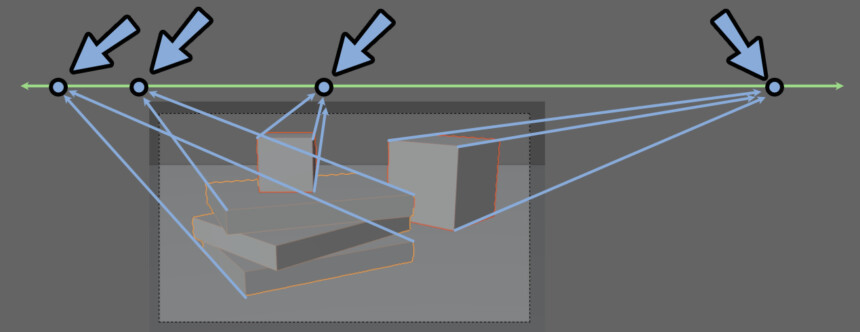
そして、1つの絵の中に複数の透視図法が混ざる事があります。
・カメラと横軸が平行な立方体は1点透視図法
・カメラと横軸が平行でない立方体は2点透視図法
(縦パースを無視した説明)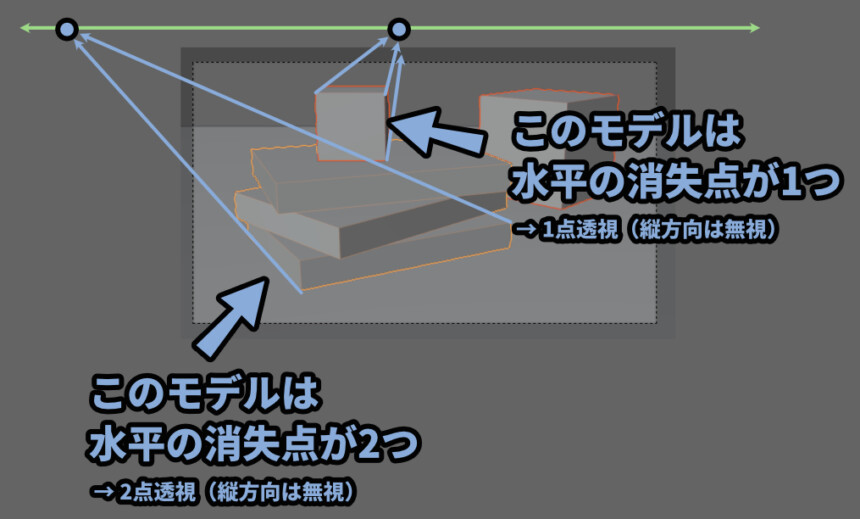

↑は厳密に言うと「3点透視図法」と「消失点が横1+縦1の2点透視図法」ですが…
そんな事を言い出すと、説明がややこしくなるので、縦方向は無視して、「2点透視」と「1点透視」で表現しました。
縦方向の消失点は見ている位置に帰結する
3点透視図法の消失点はEL上にありません。
では何処へ向かうのか…?
辿ってみると… 地面に対して平行に置かれたモノであればある1か所に向かいます。
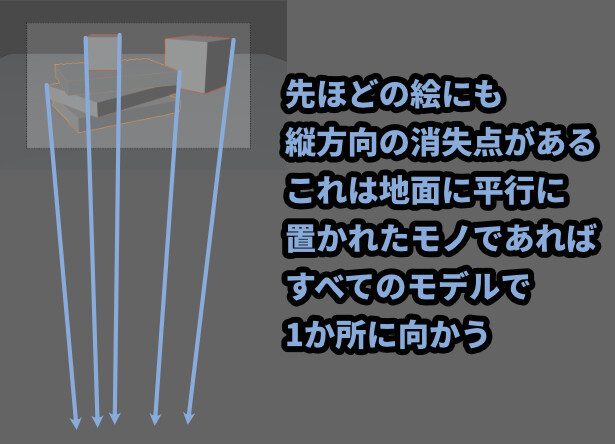
では、どこへ向かうのか。
それは基本は画像の中央、カメラがある位置です。
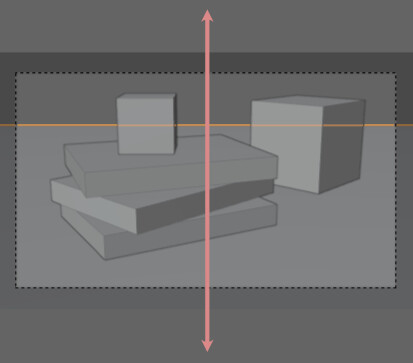

ELが視点に対して「横方向の軸上」と考えるのであれば…
縦パースは視点に対して「縦方向の軸上」と考えれます。
トリミングすると画面の中央が変わるので注意
縦パースのELがあるポイントは、視点の縦位置なので…
基本は画像の中央です。

が… 画像は一部を切り取る、トリミングという処理が行われる事があります。
これを行うと、縦パースの位置が画面の中央でなくなります。
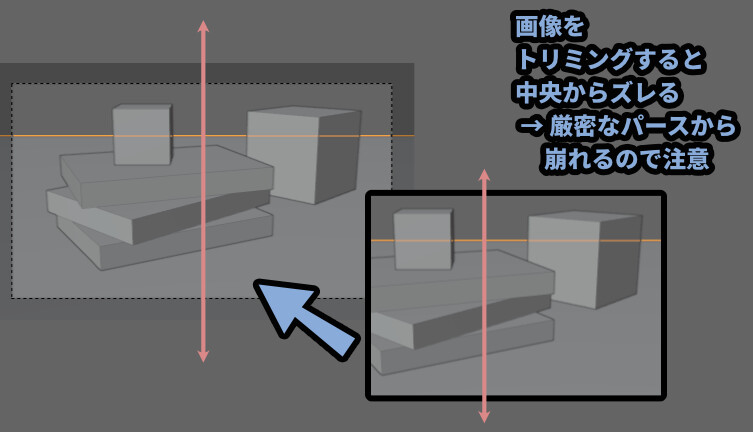
なので、カメラを上下に向けて撮影した画像をトリミングすると…
すごく厳密にいえば、縦パースの位置という点でパースが破綻した、デッサンが狂った絵になるので注意。

きっと、誰もこんなことを気にして生きてないし、
気にしても「いいね」は取れない = 評価されるポイントはここではない。
なので、そこまで気にしなくていい事ですが…
余裕があったら、静止画作品はできるだけトリミング無しで完成するよう意識してください。

トリミングした絵をPixiなどに投稿しても…
たぶん「あなたの絵、縦パースの位置狂ってますね?」や「縦パースの位置が画面中央にないので残念でした」みたいなコメントは来ない。
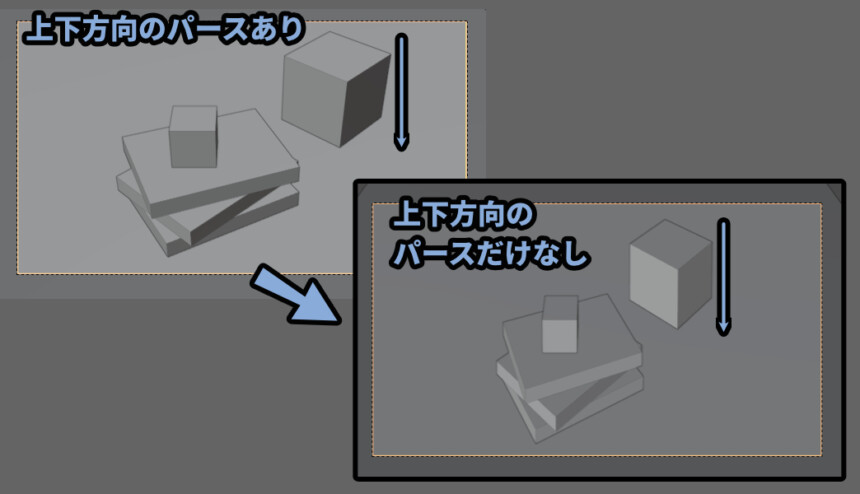
縦方向のパースだけ消す事もできる
この縦パースは特殊なレンズを使えば消せます。
そのレンズが「チルトシフトレンズ」です。
↓みたいな、レンズが曲がるレンズ。
一部の3DCGツールでは、この見え方に対応してます。
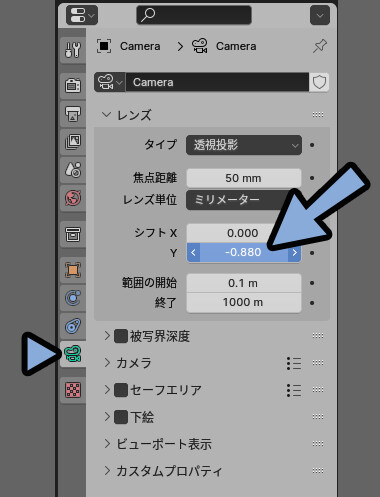
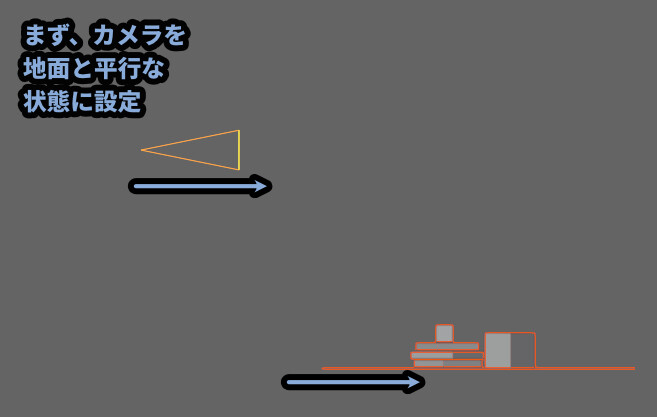
考え方としては、まずカメラ自体を上や下に回転すると縦パースが発生する。
そこで、カメラと地面を平行にして縦パースを消す。
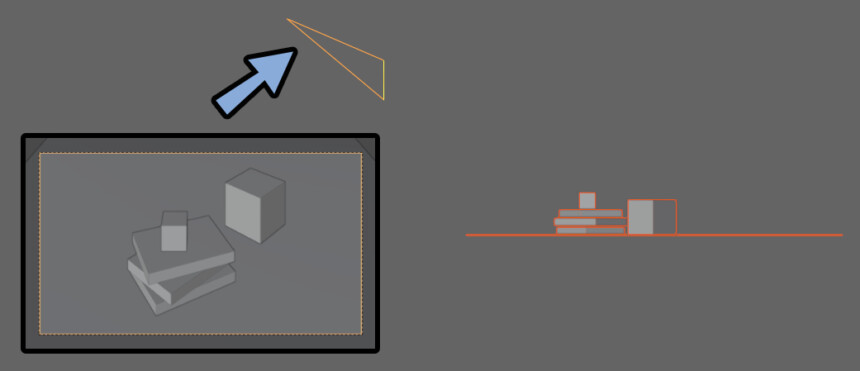
そして… カメラは回転させず、レンズだけを回転させる。
これで縦パースを解除した状態で、見上げるor見下ろすができます。

トリミングした絵をPixiなどに投稿しても…
たぶん「あなたの絵、縦パースの位置狂ってますね?」や「縦パースの位置が画面中央にないので残念でした」みたいなコメントは来ない。
私が使ってる3DCGツール、Blenderでこれを設定する方法はこちらで解説。
「近くて小さい」と「遠くて大きい」の問題
画面上に写るモノの大きさは下記の2つの要素で変更できます。
・物自体の大きさ
・カメラとの距離(近いと大きく、遠いと小さく)なので「小さいモノ×近いモノ」と「大きいモノ×遠いモノ」の組み合わせが、
ほぼ同じように見える事があります。
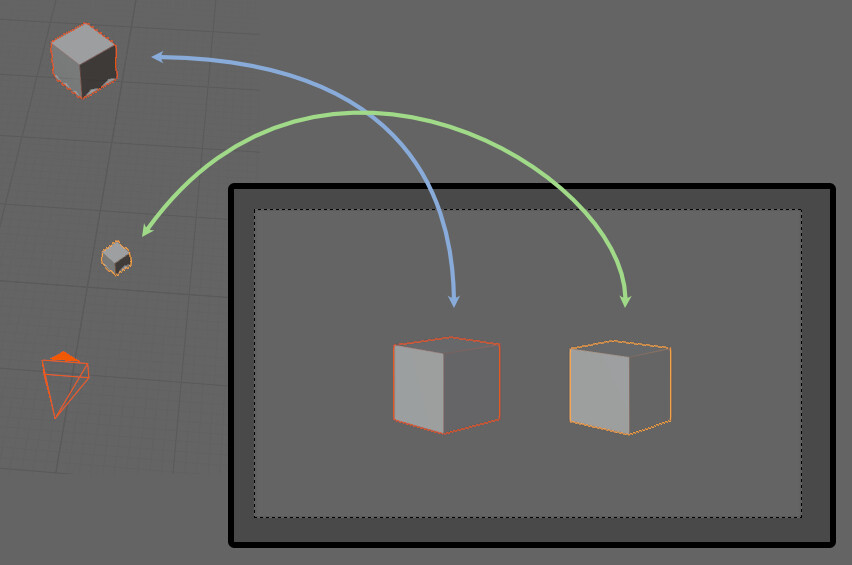
これに関しては… 諦めるしかないです。 そういうモノです。
対処法は「別の方法で距離を表現する」ことです。
【遠近法以外の距離表現のアイデア】
・比較になるモノを入れる
・空気遠近法を使う
・ピンボケを使う
…など比較になるモノで一番わかりやすいモノは地面です。
↓の絵は地面ができたことで、同じような大きさでも奥行きが分かり
遠くのモノが大きい事が分かるようになりました。
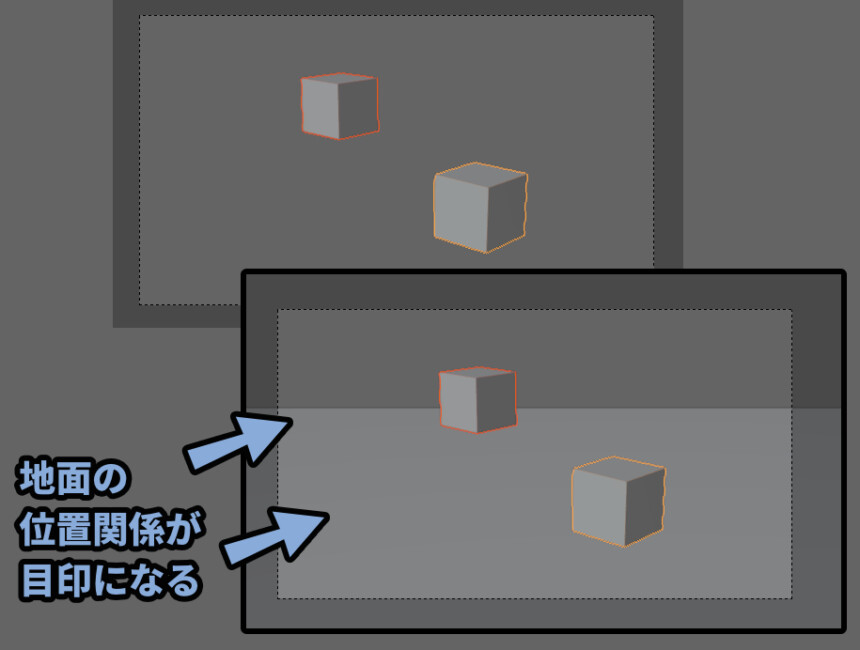
ほかにも、ピンボケや空気遠近法といった距離を表現する技法を使うと同じ大きさでも距離を伝えれます。

このような技法を使えば、「近くて小さい」と「遠くて大きい」問題に対処できます。

対処できますが… 結局、視覚的に分かりにくいので…
一番はこんな感じの紛らわしい要素の配置を避ける事。
そもそも最初から、こんな絵作りをしようとしない事をおすすめします。
4点以上の透視図法としての全円魚眼の紹介
4点透視図法以上は… ありますが私たちが思ってるようなモノではなくなります。
↓例えば、このような魚眼パースは5点透視図法と考えれます。
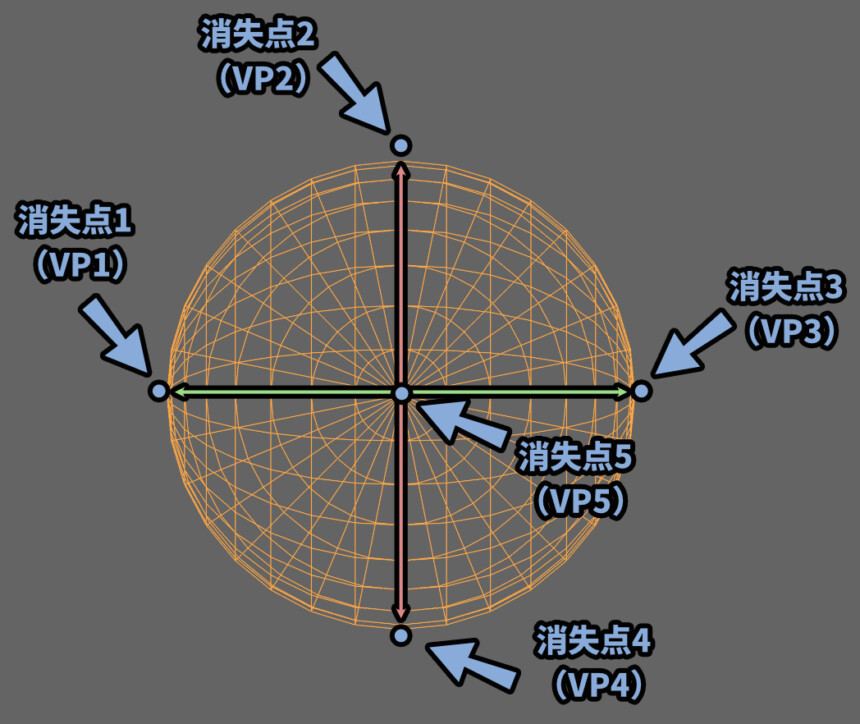
ちなみに、球体が映るモノを円周魚眼、球の一部を切り取ったものを対角魚眼と言います。
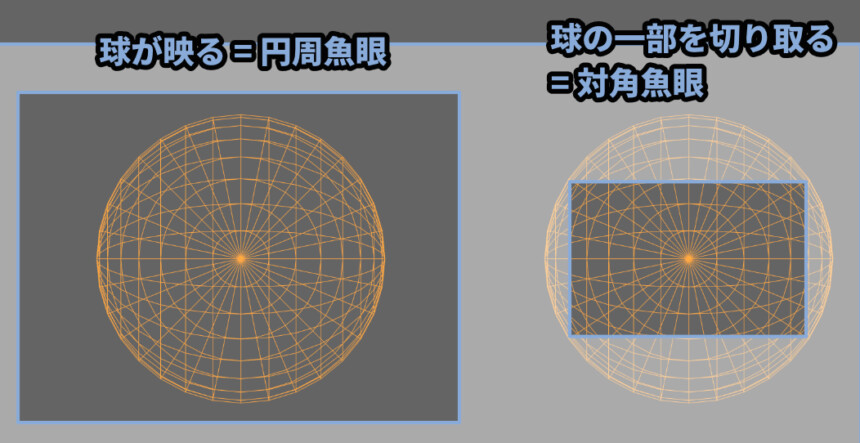
このように、4点以上の消失点ができる事があります。

ちょっと本題から離れていくので、ここでの解説はこのぐらいにします。
また、機会があったら解説します。
以上が、4点以上の透視図法としての全円魚眼の紹介です。
パースペクティブの仕組みの解説が終わったので…
次は「画角」を説明していきます。
画角について
画角は、一言でいうと視野の広さです。
カメラの写る範囲、3DCGツールのBlenderカメラで説明すると、ココの角度
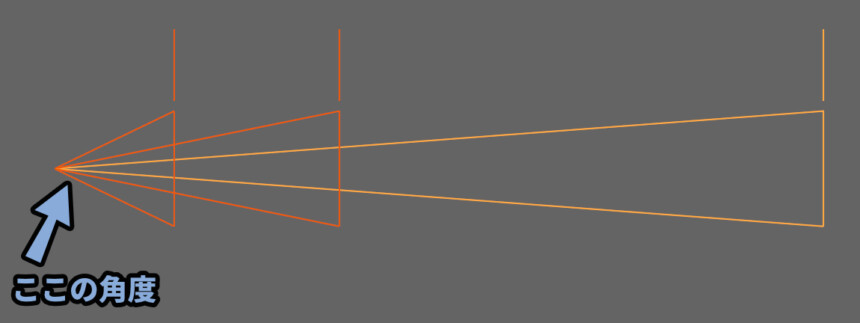
・画角、視野が広いと「広い範囲が映る」+「パースの歪みが増えます」
・画角、視野が狭いと「狭い範囲が映る」+「パースの歪みが減ります」
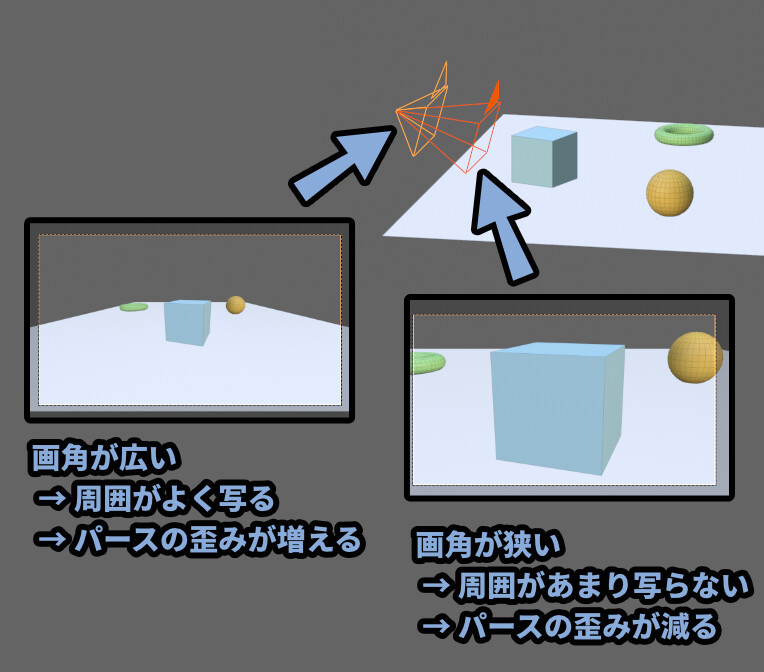
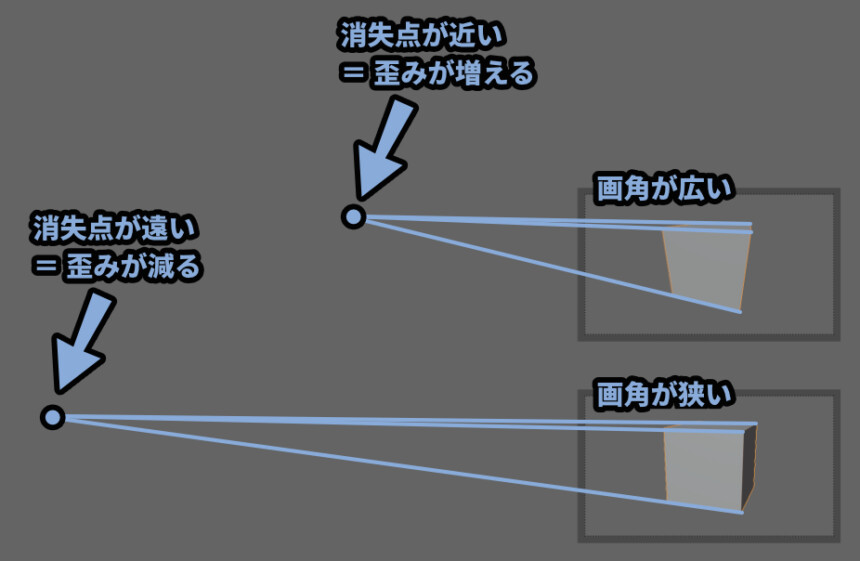
画角が広いと、消失点がカメラに近い位置に発生します。
なので、パースの歪みが増えます。
逆に画角が遠いと消失点が遠くなり、パースの歪みが減ります。
そして、この画角を連続的に変化させると…
私たちがよく使ってるカメラの「ズーム機能」になります。

以上が、画角について基本的な説明です。
「近づく事」と「ズームする事」の違い
カメラに写る被写体の大きさは下記の方法でも変化できます。
・被写体に近づく(近いと大きく、遠いと小さく)
・画角を変えてズームする(画角が狭いと大きく、広いと小さく)なので「遠い×画角が狭いモノ」と「近い×画角が広いモノ」の組み合わせを行うと…
画面的にはほぼ同じ大きさに写せます。
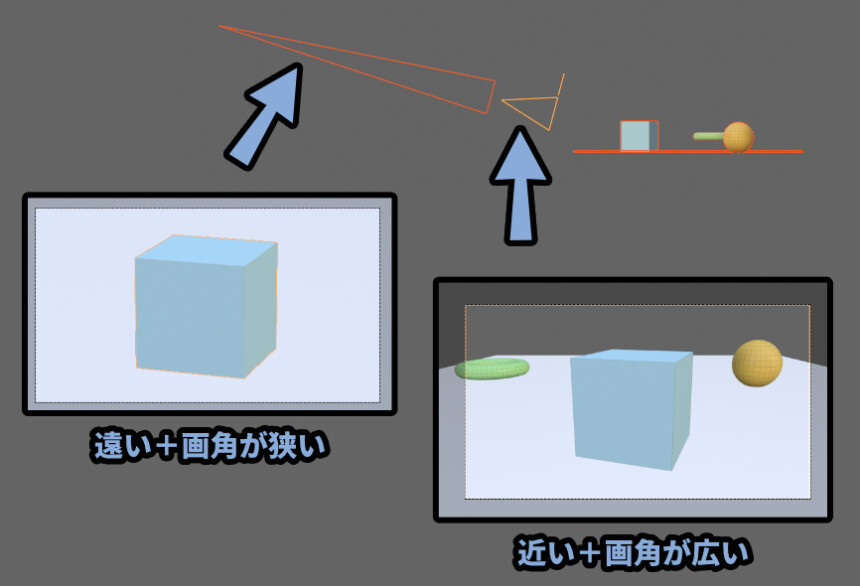
この2つの大きな違いは下記の2つ。
・周囲のモノが映るかどうか
・パースの歪みが入るかどうか狭い画角は周囲のモノが映りにくく、パースの歪みが少ないです。(消失点が画面中央に遠くなる)
広い画角は周囲のモノが映り、パースの歪みが増えます。(消失点が画面中央に近くなる)
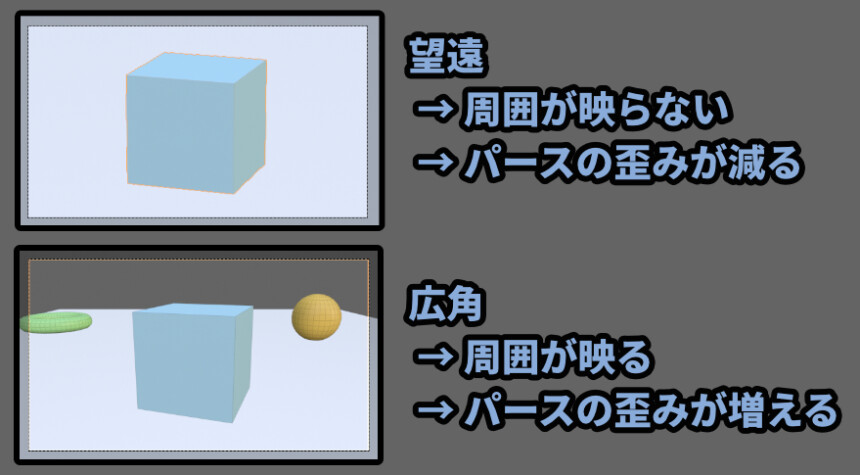
※画角が狭い=望遠、画角が広い=広角。
どちらがを使うのが良いかは、作りたい絵次第です。

・望遠 → 歪みが少ないので萌えキャラを可愛く見せるのに向いている
・広角 → 広くて壮大な景色を見せるのに向いている
キャラの場合、造形が歪み可愛さが減る
以上が「近づく事」と「ズームする事」の違いです。
広角の果てが「魚眼」や「HDRI」
広角の果てが魚眼パースやHDRIと呼ばれる画像です。
この広角の果ては「視野角を広げる」を考える事で理解できます。
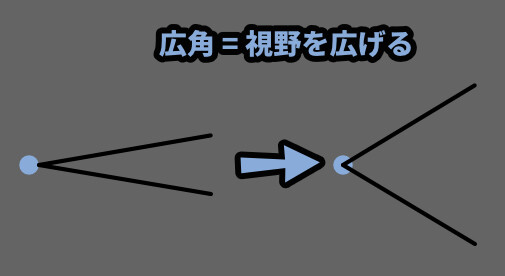
そして、魚眼は視野角が180度ぐらいになったモノです。
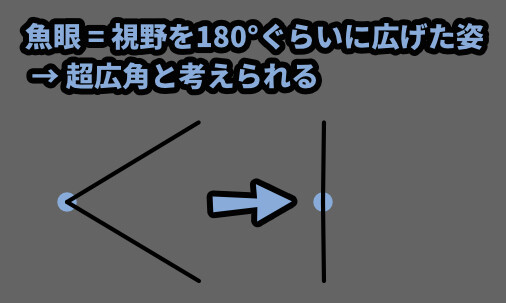
つまり、魚眼パースの絵はパース歪みを極めて、超広大な景色を写してると考えれます。

そして、3DCG系にはHDRIという形式の画像があります。
これは… より世界をゆがめ、360度の風景を1枚の画像に収めてます。(作例)
先ほどの図で表すと、このようなイメージ。
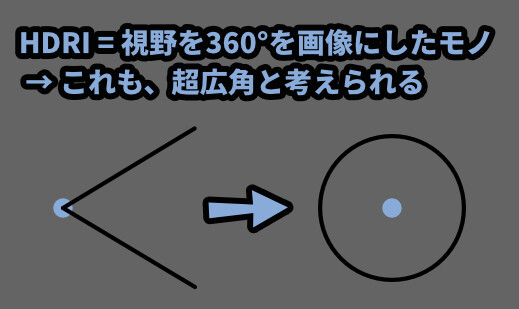
以上が、広角の果てが「魚眼」や「HDRI」という紹介です。
望遠の果てが平行投影
広角の果てが平行投影と呼ばれる透視図法です。
この望遠の果ては「望遠で消失点が遠のき、歪みが減る」事を考えると理解できます。

現実では不可能ですが… 3DCGでは、このパースの歪みが0の状態を作れます。
それが平行投影です。

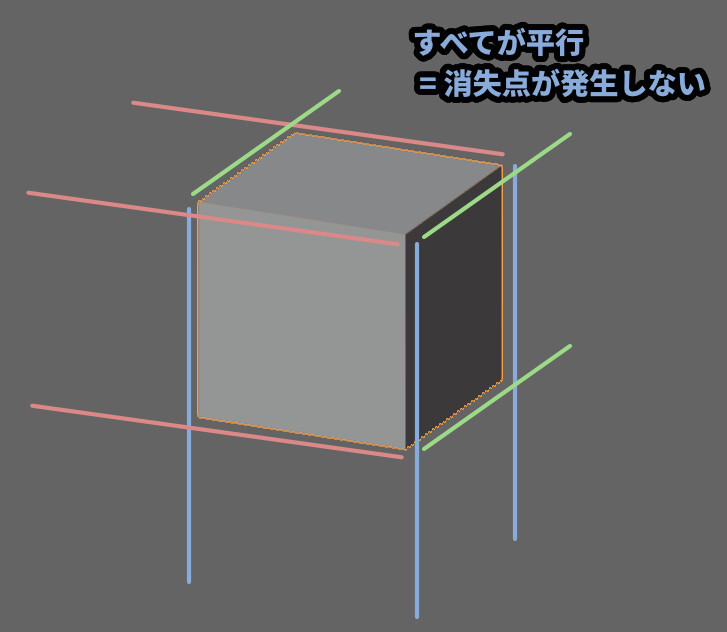
これは、下図のように平行な線に消失点が発生しないという特徴があります。
つまり、消失点が無限遠に遠のき、パースの歪みが0になった状態です。
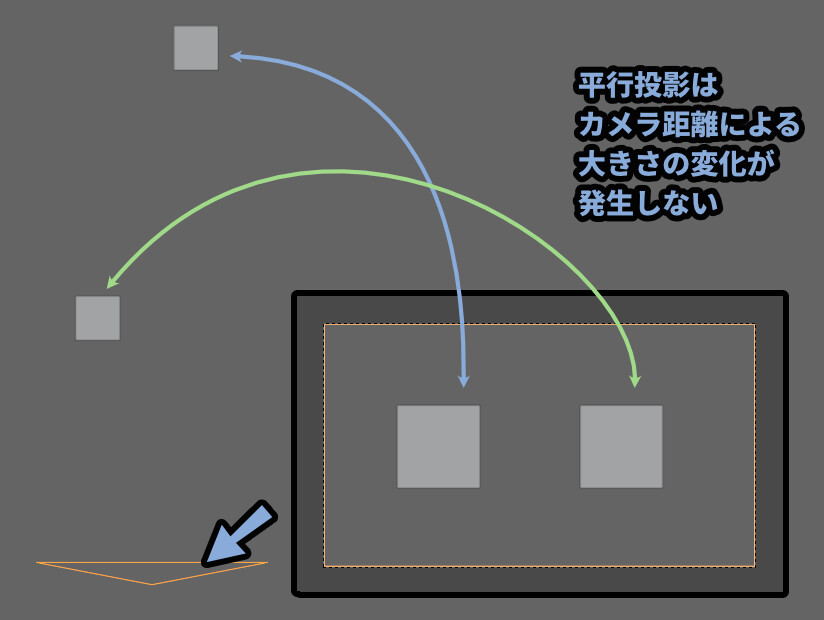
そして、平行投影はカメラの距離によって大きさが変化しないという特徴があります。
消失点は大きさの変化を連続的にした先に発生するモノなので…
消失点が発生しない = 大きさの変化が発生しないという意味になります。

現実では不可能なので、超望遠レンズを使って似たような形にするしか手はありませんが…
3DCGでは、このような現実を超えた表現もできます。
以上が、望遠の果てが「平行投影」という説明です。
3つの画角の表記方法
主な画角の表記方法は3つ。
・焦点距離(mm)
・視野角(°)
・倍率(n倍)この3つを解説します。
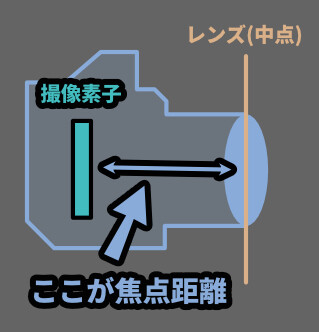
焦点距離(mm)
これは… カメラの中にある光を記録する装置~レンズのまでの距離で画角を表します。
これ、最も一般的な画角を表す単位です。
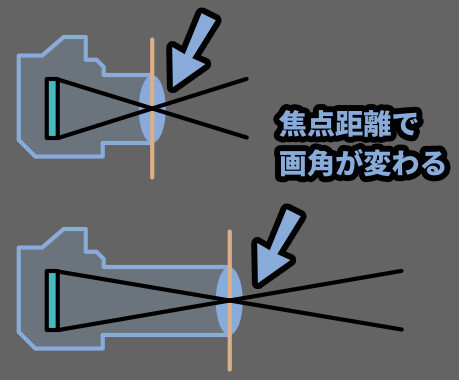
この焦点距離が変わると、画角が変わります。
近いと画角が広く、遠いと画角が狭くなります。
主にカメラや3DCGに使われます。
↓の800mmのように。
3DCGも同じように焦点距離が画角の「mm」で表現されてるモノが多いです。
基本的に使うのはこの「mm」表記の単位です。
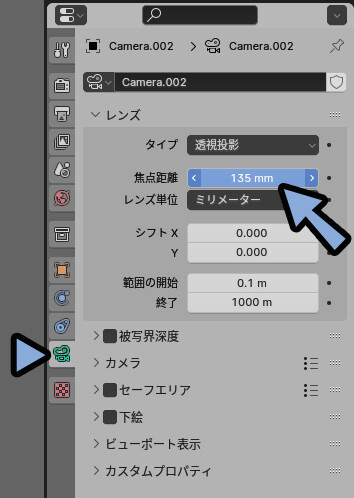
直感的でなくて申し訳ないですが…
慣れるとこのmmの数字で大体の絵がイメージできます。

ちなみに、人間の目の焦点距離は「50mm」とされています。
この50mmが「標準レンズ」です。
→ それより数字が小さいモノが「広角レンズ」
→ それより数字が大きいモノが「望遠レンズ」
…という扱いになります。
撮像素子の大きさの考え方
光を記録する装置の大きさで画角が変わります。
一般的な画角のmm表示は、 “フルサイズ” と呼ばれる規格、横幅35mmセンサーの大きさで計算されてます。
//ーーーーー
35mmの大きさが基準になったのは…
フィルムカメラ時代に、一番よく使われたこの形のフィルムが名残。
ちなみに、35mmフィルムの大きさは「36×24mm」で厳密には35mmでは無いです。
が、上手く写らない範囲などの余白を含めて35mmと表現されてます。(たぶん)

フィルムカメラ時代も「中判フィルム(60×45mmなど)」や「シノゴフィルム(100×125mm)」の大きさの違う撮像素子、フィルムがありました。
↓のレンズを指すところの中にあるデカイ四角形が…
「フルサイズ」のイメージセンサー、撮像素子です。
もちろん、フルサイズでは無いカメラもあります。例えば…
↓のレンズを指すところの中にあるちょっと小さくなった四角形が…
「APS-C」サイズのイメージセンサー、撮像素子です。
フルサイズのカメラ以外の焦点距離もmmで表示されます。
そしてこちらは、「フルサイズ換算」や「35mm equiv.」など表記がされてます。


・35mm equiv. → 要約すると、フルサイズ換算の意味。
・35mm = フルサイズの撮像素子の大きさを表す
・equiv. = equivalentの意味 → 訳すと「相当する、等質の」など。
以上が撮像素子の大きさの考え方です。
視野角(°)
これは、視点から見える範囲を角度で表したモノです。
これも表現は違いますが、画角を意味します。
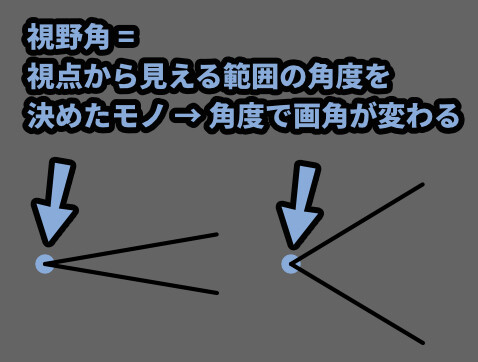
この単位は主に一人称視点の3DCGの “ゲーム” に使われます。
3DCGでも設定すれば使えるモノもあります。
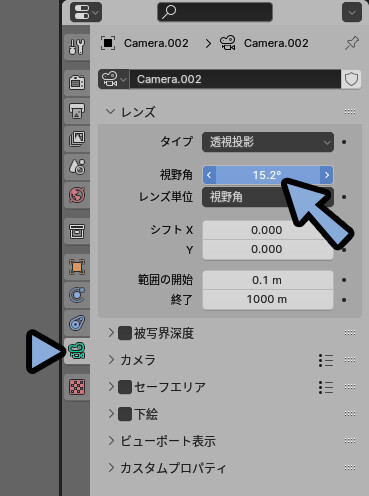

ちなみに、人間の目の視野角は…
左右両目の扱いをどうするかで違い
具体的にn°のような数字は無いようです。
ただ、焦点距離=50mmから視野角は割り出せば、
視野角は「46°」になるようです。
※一部では「47°」と表記してました。
倍率(n倍)
これはある画角を基準にして、ズームしn倍の大きさに見えるという意味。
基本的には人の目の画角を50mmとし、そこからn倍のような形で表されます。
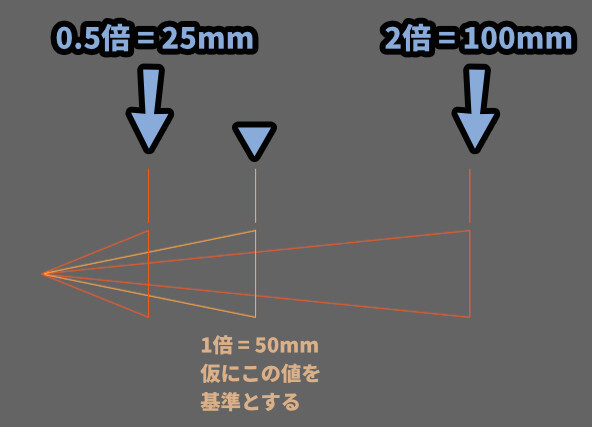
この単位は、主に “双眼鏡” で使われます。
↓の双眼鏡は「8倍」と書かれてます。
つまり… これが表す意味と画角は下記。
・双眼鏡の倍率は、人間の目を基準にして「× n倍」する
・人間の目=焦点距離「50mm」
・「50mm」×「8倍」なら… = 400mm相当
双眼鏡の値もあくまで “目安” なので注意。
細かくはメーカーによって異なる事があります。
倍率ズームの場合
超望遠のコンデジなどの “カメラ” には「n倍ズーム」と表記されることがあります。
これは… 双眼鏡の「n倍」と意味が変わるので注意。
【n倍】
・双眼鏡で使われる倍率
・人間の目(50mm)を基準に「× n倍」して計算できる
【n倍ズーム】
・一部のカメラで使われるの倍率
・そのカメラの最小の画角を基準にして「× n倍」して計算する↓このカメラでは光学65倍ズームと書かれてます。
これは、人間の目の画角50mmを65倍した3250mmという意味ではないです。
このカメラの最小焦点距離が21mm。
そこに×65して…「1365mm」という事を表してます。

なので… このカメラの光学ズーム65倍は…
「21~1365mmまでズームイン/ズームアウトできます」という意味になります。

「n倍」と「n倍ズーム」の2つは似てますが…
別物なので注意してください。
まとめ
今回は、遠近法、カメラの画角とパースペクティブの考え方について紹介しました。
・近くのモノは大きく、遠くのモノは小さく写る
・距離のよる大きさの変化を連続的にすると消失点が発生する
・地面対して平行+角が90度のモノでは1~3透視図法が成立する
・横方向の消失点は目の高さによって発生した横線、アイレベル上に集まる
・縦方向の消失点は視点の位置、基本的に画面中央に集まる
・画角は写る範囲と、遠近法による歪みの強度を変える
・画角が広い=広角だと広い範囲が映るがモノが歪む
・画角が狭い=望遠だと狭い範囲しか映らないが、モノの歪みが軽減される
・広角の果てが魚眼やHDIR、望遠の果てが平行投影
・画角は焦点距離(mm)か視野角(°)で表される
また、他にも絵作りに関係ある事を発信してます。
ぜひ、こちらもご覧ください。




コメント